题目大意就是给出n和k求出第k个与n互素的数(当然不能暴力的啊)因为k很大
首先要知道这个知识
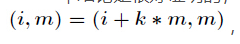
题意:求(1--N!)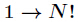
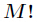
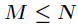
解析:既然M<=N,所以(N!)%(M!)==0,我们可以得到这个结论


所以这个题就是找到这个解决了
#pragma GCC optimize(1) #pragma GCC optimize(2) #pragma GCC optimize(3,"Ofast","inline") #include<cstring> #include<cstdio> #include<iostream> #include<queue> #include<algorithm> using namespace std; typedef long long ll; template <typename Tp> void read(Tp &x){//read(n); x=0;char ch=1;int fh; while(ch!='-'&&(ch>'9'||ch<'0')){ ch=getchar(); } if(ch=='-'){ fh=-1;ch=getchar(); }else fh=1; while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+ch-'0';ch=getchar(); } x*=fh; } inline char read1()//字符串读入挂 { register char ch=getchar(); while(ch<'A'||ch>'M')ch=getchar(); return ch; } const int maxn=1e6+100; const int mod=1000000007; int gcd(int a,int b){ if(b==0){ return a; } return gcd(b,a%b); } int a[maxn]; int main(){ int m,k; while(~scanf("%d%d",&m,&k)){ int cnt=0; for(register int i=1;i<=m;i++){ if(gcd(i,m)==1){ a[++cnt]=i; } } if(k%cnt==0){ printf("%lld ",(k/cnt-1)*m+a[cnt]); } else{ printf("%lld ",(k/cnt)*m+a[k%cnt]); } } }