小浣熊在银河护卫队的一次巡航中发现了一个神秘的星系,恰巧它所在星系和神秘星系关于笔直的分界线对称,我们将这种星系称为对称星系。
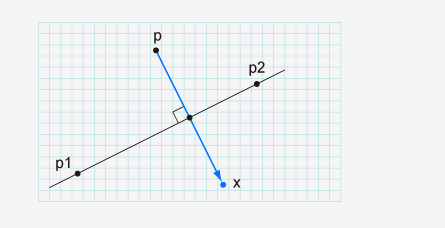
对于给定的三个点p1,p2,p,找到p的反射点x。
输入
第一行中,给出了p1和p2的整数坐标。
第二行中,给出p的整数坐标的Q个查询。(0<Q<1000)
接下来每行有一个p的x,y坐标。
(对于所有点的坐标(Xi,Yi)都是-10000<Xi,Yi<10000小数)
输出
对于每个查询,打印反射点x的坐标。( 输出值保留整数)
样例输入 Copy
0 0 2 0 3 -1 1 0 1 1 1
样例输出 Copy
-1 -1 0 -1 1 -1
#include "bits/stdc++.h" #define hhh printf("hhh ") #define see(x) (cerr<<(#x)<<'='<<(x)<<endl) using namespace std; typedef long long ll; typedef pair<int,int> pr; inline int read() {int x=0,f=1;char c=getchar();while(c!='-'&&(c<'0'||c>'9'))c=getchar();if(c=='-')f=-1,c=getchar();while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();return f*x;} const int maxn = 1e9+7; const int inf = 0x3f3f3f3f; const int mod = 1e8+7; int main() { double x1,y1,x2,y2; cin>>x1>>y1>>x2>>y2; int t; cin>>t; while(t--){ double x3,y3,x4,y4; cin>>x3>>y3; if(x2==x1&&y2==y1){ x4=2*x1-x3; y4=2*y1-y3; } else if(x2==x1||y2==y1){ if(x2==x1){ y4=y3; x4=2*x1-x3; } else{ x4=x3; y4=2*y2-y3; } } else{ double k1=(y2-y1)/(x2-x1); if((y3-y1)==k1*(x3-x1)){ int x=(int)x3; int y=(int)y3; printf("%d %d ",x,y); continue; } double k2=-(1.0)/k1; x4=((k1+k2)*x3+2*(y2-y3-k1*x2))/(k2-k1); y4=k2*(x4-x3)+y3; } int x=(int)(x4); int y=(int)(y4);//注意取整 printf("%d %d ",x,y); } return 0; }