[数据结构

一、什么是单链表？

单链表：使用链式存储结构的线性表。单链表中的数据是以结点来表示的，每个结点的构成：数据域（数据元素的映像） + 指针域（指示后继元素存储位置）。如果单链表不做特别说明，一般指的是动态单链表。

在 C 语言中可用结构指针来描述单链表：

/* 线性表的单链表存储结构 */
typedef struct node
{
	ElemType data;
	struct node *next;
}Node, LinkList;

从这个结构定义中可以看出，结点由存放数据元素的数据域和存放后继结点地址的指针域组成。

空链表的示意图：

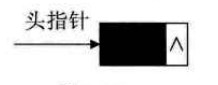
带有头结点的单链表：

不带头结点的单链表的存储结果示意图：

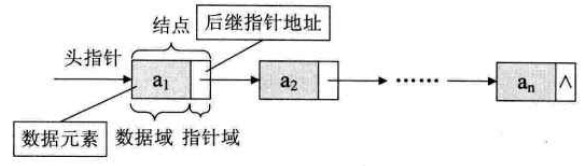
二、单链表的基本操作

2.1 插入操作

单链表的插入操作核心代码只有两句（例如在结点 p 后面插入结点 s）：

s->next = p->next; // 将p的后继结点赋值给s的后继
p->next = s; // 将s赋值给p的后继结点

解读这两句代码，也就是说让 p 的后继结点改成 s 的后继结点，再把结点 s 变成 p 的后继结点，如下图所示：

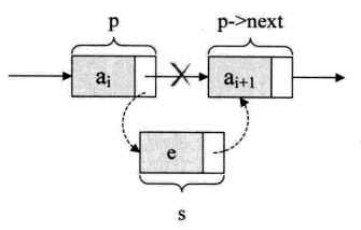
单链表第 i 个位置插入结点的算法思路：

声明一结点 front 指向链表头结点，初始化 j 从 1 开始；
当 j<i 时，就遍历链表，让 front 的指针向后移动，不断指向下一结点，j 累加 1；
若到链表末尾 front 为空，则说明第 i 个元素不存在；
否则查找成功，在系统中创建一个空结点 pTemp；
将数据元素 e 赋值给pTemp->data；
执行单链表的插入结点语旬pTemp->next = front ->next、front->next=pTemp；
返回成功。

实现代码如下:

// 插入元素操作
Status insertList(LinkList *pList, int i, const ElemType e)
{
	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}
	// 只能在位置1以及后面插入，所以i至少为1
	if (i < 1)
	{
		printf("i is invalid!
");
		return FALSE;
	}

	// 找到i位置所在的前一个结点
	Node *front = pList; // 这里是让front与i不同步，始终指向j对应的前一个结点
	for (int j = 1; j < i; j++) // j为计数器，赋值为1，对应front指向的下一个结点，即插入位置结点
	{
		front = front->next;
		if (front == NULL)
		{
			printf("dont find front!
");
			return FALSE;
		}
	}
		
	// 创建一个空节点，存放要插入的新元素
	Node *temp = (Node *)malloc(sizeof(Node));
	if (!temp)
	{
		printf("malloc error!
");
		return FALSE;
	}
	temp->data = e;

	// 插入结点
	temp->next = front->next;
	front->next = temp;

	return TRUE;
}

实现的难点在于：如何找到要插入的 i 位置所在的前一个结点。
注意：这里是有头结点的，头结点的位置为0，所以插入位置不能为0，至少为1。
当 i=1 时，则能够不进入 while，且 front 指向头结点，后面直接在头结点后面即位置 1 插入元素 e。
当 i=2 时，则控制只进入 while 一次，且 front 指向第一个存放元素的结点，在位置 2 插入元素 e。

2.2 删除操作

单链表的删除操作核心代码只有一句（删除结点 p 后面一个结点）：

p->next = p->next->next; // 将p的后继结点的后继赋值给p的后继

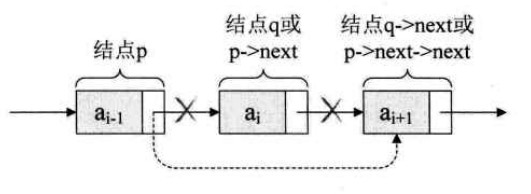
单链表第 i 个数据之后删除结点的算法思路（删除的是 i+1 位置的结点）：

声明一结点 front 指向链表头结点，初始化 j 从 1 开始；
当 j<i 时，就遍历链表，让 front 的指针向后移动，不断指向下一个结点，j 累加1；
若到链表末尾 front 为空，则说明第 i 个元素不存在；
否则查找成功，查找到要删除位置的前一个结点 front，并赋值给 pTemp；
执行链表的删除结点语句front->next = front->next->next；
将 pTemp 结点中的数据赋值给 e，作为返回;
释放 pTemp 结点，并指向 NULL;
返回成功。

实现代码如下：

// 删除元素操作
Status deleteList(LinkList *pList, int i, ElemType *e)
{
	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}
	// 只能删除位置1以及以后的结点
	if (i < 1)
	{
		printf("i is invalid!
");
		return FALSE;
	}

	// 找到i位置所在的前一个结点
	Node *front = pList; // 这里是让front与i不同步，始终指向j对应的前一个结点
	for (int j = 1; j < i; j++) // j为计数器，赋值为1，对应front指向的下一个结点，即插入位置结点
	{
		front = front->next;
		if (front->next == NULL)
		{
			printf("dont find front!
");
			return FALSE;
		}
	}

	// 提前保存要删除的结点
	Node *temp = front->next;
	*e = temp->data; // 将要删除结点的数据赋给e

	// 删除结点
	front->next = front->next->next;

	// 销毁结点	
	free(temp);
	temp = NULL;

	return TRUE;
}

实现的难点在于：如何找到要删除的 i 位置所在的前一个结点。

2.3 头部插入与尾部插入操作

头部插入，就是始终让新结点在第一个结点的位置，这种算法简称为头插法，如下图所示：

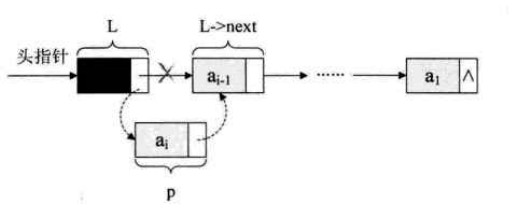
实现代码如下：

// 头部后插入元素操作
Status insertListHead(LinkList *pList, const ElemType e)
{
	Node *head;
	Node *temp;

	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}

	// 让head指向链表的头结点
	head = pList;

	// 创建存放插入元素的结点
	temp = (Node *)malloc(sizeof(Node));
	if (!temp)
	{
		printf("malloc error!
");
		return FALSE;
	}
	temp->data = e;
	
	// 头结点后插入结点
	temp->next = head->next;
	head->next = temp;

	return TRUE;
}

尾部插入，将数据元素插入到尾节点后面，这种简称为尾插法，如下图所示：

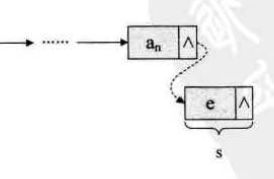
实现代码如下：

// 尾部后插入元素操作
Status insertListTail(LinkList *pList, const ElemType e)
{
	Node *cur;
	Node *temp;

	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}

	// 找到链表尾节点
	cur = pList;
	while (cur->next)
	{
		cur = cur->next;
	}

	// 创建存放插入元素的结点
	temp = (Node *)malloc(sizeof(Node));
	if (!temp)
	{
		printf("malloc error!
");
		return -1;
	}
	temp->data = e;

	// 尾结点后插入结点
	temp->next = cur->next;
	cur->next = temp;

	return TRUE;
}

2.4 清空链表操作

清空链表的算法思路如下:

声明一结点 cur 和 temp;
将第一个结点赋值给 cur ;
循环：
- 使用 temp 事先保存下一结点，防止后面释放 cur 后导致“掉链”;
- 释放 cur;
- 将 next 赋值给 cur。

实现代码算法如下：

// 清空链表操作
Status clearList(LinkList *pList)
{
	Node *cur; // 当前结点
	Node *temp; // 事先保存下一结点，防止释放当前结点后导致“掉链”

	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}

	cur = pList->next; // 指向第一个结点
	while (cur)
	{
		temp = cur->next; // 事先保存下一结点，防止释放当前结点后导致“掉链”
		free(cur); // 释放当前结点
		cur = temp; // 将下一结点赋给当前结点p
	}
	pList->next = NULL; // 头结点指针域指向空

	return TRUE;
}

三、完整程序

#include <stdio.h>
#include <stdlib.h>

#define TRUE 1
#define FALSE 0
typedef int Status; // Status是函数结果状态，成功返回TRUE,失败返回FALSE

typedef int ElemType;
/* 线性表的单链表存储结构 */
typedef struct node
{
	ElemType data;
	struct node *next;
}Node, LinkList;

void initList(LinkList **pList); // 初始化链表操作
Status insertList(LinkList *pList, int i, const ElemType e); // 插入元素操作
Status deleteList(LinkList *pList, int i, ElemType *e); // 删除元素操作
Status getElem(LinkList *pList, int i, ElemType *e); // 获取元素操作
Status insertListHead(LinkList *pList, const ElemType e); // 头部后插入元素操作
Status insertListTail(LinkList *pList, const ElemType e); // 尾部后插入元素操作
Status clearList(LinkList *pList); // 清空链表操作
void traverseList(LinkList *pList); // 遍历链表操作

// 初始化单链表操作
void initList(LinkList **pList) // 必须使用双重指针，一重指针申请会出错
{
	*pList = (LinkList *)malloc(sizeof(Node));
	if (!pList)
	{
		printf("malloc error!
");
		return;
	}

	(*pList)->data = 0;
	(*pList)->next = NULL;
}

// 插入元素操作
Status insertList(LinkList *pList, int i, const ElemType e)
{
	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}
	// 只能在位置1以及后面插入，所以i至少为1
	if (i < 1)
	{
		printf("i is invalid!
");
		return FALSE;
	}

	// 找到i位置所在的前一个结点
	Node *front = pList; // 这里是让front与i不同步，始终指向j对应的前一个结点
	for (int j = 1; j < i; j++) // j为计数器，赋值为1，对应front指向的下一个结点，即插入位置结点
	{
		front = front->next;
		if (front == NULL)
		{
			printf("dont find front!
");
			return FALSE;
		}
	}
		
	// 创建一个空节点，存放要插入的新元素
	Node *temp = (Node *)malloc(sizeof(Node));
	if (!temp)
	{
		printf("malloc error!
");
		return FALSE;
	}
	temp->data = e;

	// 插入结点
	temp->next = front->next;
	front->next = temp;

	return TRUE;
}

// 删除元素操作
Status deleteList(LinkList *pList, int i, ElemType *e)
{
	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}
	// 只能删除位置1以及以后的结点
	if (i < 1)
	{
		printf("i is invalid!
");
		return FALSE;
	}

	// 找到i位置所在的前一个结点
	Node *front = pList; // 这里是让front与i不同步，始终指向j对应的前一个结点
	for (int j = 1; j < i; j++) // j为计数器，赋值为1，对应front指向的下一个结点，即插入位置结点
	{
		front = front->next;
		if (front->next == NULL)
		{
			printf("dont find front!
");
			return FALSE;
		}
	}

	// 提前保存要删除的结点
	Node *temp = front->next;
	*e = temp->data; // 将要删除结点的数据赋给e

	// 删除结点
	front->next = front->next->next;

	// 销毁结点	
	free(temp);
	temp = NULL;

	return TRUE;
}

// 获取元素操作
Status getElem(LinkList *pList, int i, ElemType *e)
{
	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}
	// 只能获取位置1以及以后的元素
	if (i < 1)
	{
		printf("i is invalid!
");
		return FALSE;
	}

	// 找到i位置所在的结点
	Node *cur = pList->next; // 这里是让cur指向链表的第1个结点，与j同步
	for (int j = 1; j < i; j++) // j为计数器，赋值为1，对应cur指向结点
	{
		cur = cur->next;
		if (cur == NULL)
		{
			printf("dont find front!
");
			return FALSE;
		}
	}

	// 取第i个结点的数据
	*e = cur->data;

	return TRUE;
}

// 头部后插入元素操作
Status insertListHead(LinkList *pList, const ElemType e)
{
	Node *head;
	Node *temp;

	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}

	// 让head指向链表的头结点
	head = pList;

	// 创建存放插入元素的结点
	temp = (Node *)malloc(sizeof(Node));
	if (!temp)
	{
		printf("malloc error!
");
		return FALSE;
	}
	temp->data = e;
	
	// 头结点后插入结点
	temp->next = head->next;
	head->next = temp;

	return TRUE;
}

// 尾部后插入元素操作
Status insertListTail(LinkList *pList, const ElemType e)
{
	Node *cur;
	Node *temp;

	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}

	// 找到链表尾节点
	cur = pList;
	while (cur->next)
	{
		cur = cur->next;
	}

	// 创建存放插入元素的结点
	temp = (Node *)malloc(sizeof(Node));
	if (!temp)
	{
		printf("malloc error!
");
		return -1;
	}
	temp->data = e;

	// 尾结点后插入结点
	temp->next = cur->next;
	cur->next = temp;

	return TRUE;
}

// 清空链表操作
Status clearList(LinkList *pList)
{
	Node *cur; // 当前结点
	Node *temp; // 事先保存下一结点，防止释放当前结点后导致“掉链”

	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return FALSE;
	}

	cur = pList; // 指向头结点
	while (cur)
	{
		temp = cur->next; // 事先保存下一结点，防止释放当前结点后导致“掉链”
		free(cur); // 释放当前结点
		cur = temp; // 将下一结点赋给当前结点p
	}
	pList->next = NULL; // 头结点指针域指向空

	return TRUE;
}

// 遍历链表操作
void traverseList(LinkList *pList)
{
	// 判断链表是否存在
	if (!pList)
	{
		printf("list not exist!
");
		return;
	}

	Node *cur = pList->next;
	while (cur != NULL)
	{
		printf("%d ", cur->data);
		cur = cur->next;
	}
	printf("
");
}

int main()
{
	LinkList *pList;

	// 初始化链表
	initList(&pList);
	printf("初始化链表!

");

	// 插入结点
	insertList(pList, 1, 0);
	printf("在位置1插入元素0
");
	insertList(pList, 2, 1);
	printf("在位置2插入元素1
");
	insertList(pList, 3, 2);
	printf("在位置3插入元素2

");

	// 删除结点
	int val;
	deleteList(pList, 2, &val);
	printf("删除位置2的结点，删除结点的数据为： %d
", val);
	printf("
");

	// 头部后插入元素
	insertListHead(pList, 5);
	printf("头部后插入元素5

");

	// 尾部后插入元素
	insertListTail(pList, 8);
	printf("尾部后插入元素8

");

	// 遍历链表并显示元素操作
	printf("遍历链表：");
	traverseList(pList);
	printf("
");

	// 销毁链表
	clearList(pList);
	printf("销毁链表

");

	return 0;
}

输出结果如下图所示：

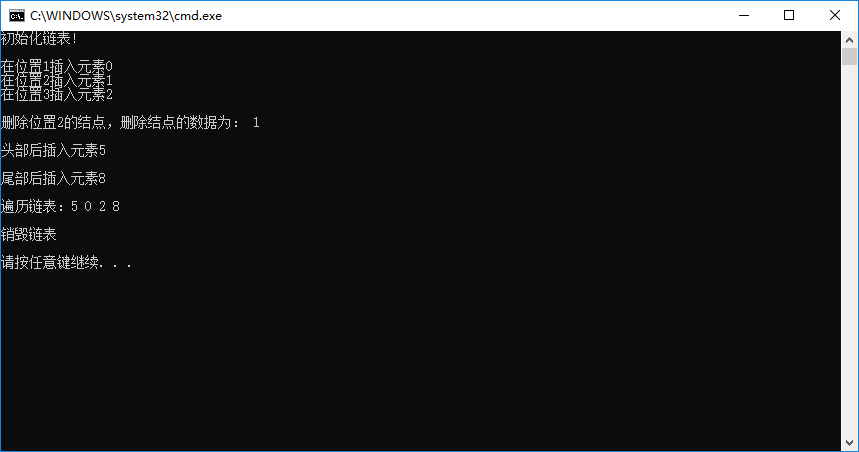
注意上面只是 “静态单链表” 的 C 语言实现，测试编译器为 VS2013。

四、单链表结构与顺序存储结构的优缺点

**经验性结论： **

1.若线性表需要频繁查找，很少进行插入和删除操作时，宜采用顺序存储结构；若需要频繁插入和删除时，宜采用链式存储结构。比如用户注册的个人信息，除了注册时插入数据外，绝大多数都是读取，所以应该考虑用顺序存储结构。

2.当线性表中的元素个数变化较大或者根本不知道有多大时，最好用链式存储结构，这样可以不需要考虑存储空间的大小问题。

参考：

《大话数据结构 - 第3章》线性表

相关阅读:
Java HashMap存储问题
 <转>堆和栈的区别
 Linux shell命令
 DNS(三)DNS SEC(域名系统安全扩展)
DNS (二)协议
 绕过CDN查找网站真实IP方法
 stream流思想应用
 http接口实现附件对接
 AQS深入分析
 AQS快速入门
原文地址：https://www.cnblogs.com/linuxAndMcu/p/10306664.html