一、线性回归
1.api

2、性能评估


3、案例(波士顿房价预测)
代码:
from sklearn.datasets import load_boston from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LinearRegression,SGDRegressor from sklearn.metrics import mean_squared_error def demo(): #获取数据 boston = load_boston() #数据划分 x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, train_size=0.25) #分别对特征值和目标值标准化 s1 = StandardScaler() x_train = s1.fit_transform(x_train) x_test = s1.transform(x_test) s2 = StandardScaler() y_train = s2.fit_transform(y_train.reshape(-1, 1)) #reshape为二维数组-1为不知样本数量,1为每个样本有一个目标值 y_test = s2.transform(y_test.reshape(-1, 1)) #---------使用正规方程预测------------- lr = LinearRegression() lr.fit(x_train, y_train) print(lr.coef_) #计算出来的w值 y_lr_predict = lr.predict(x_test) print("每个样本的预测价格:",s2.inverse_transform(y_lr_predict)) print("正规方程的均方误差:",mean_squared_error(s2.inverse_transform(y_test),s2.inverse_transform(y_lr_predict))) # ---------使用梯度下降预测------------- sgd = SGDRegressor() sgd.fit(x_train, y_train) print(sgd.coef_) # 计算出来的w值 y_sgd_predict = s2.inverse_transform(sgd.predict(x_test)) print("每个样本的预测价格:", y_sgd_predict) print("梯度下降的均方误差:", mean_squared_error(s2.inverse_transform(y_test),y_sgd_predict)) if __name__ == "__main__": demo()
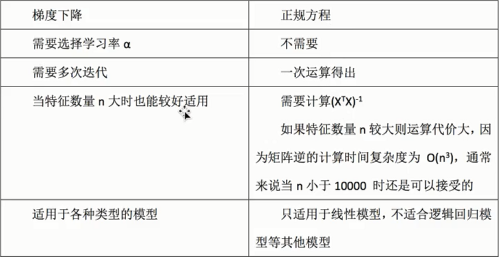
4、正规方程和梯度下降区别

5、过拟合和欠拟合


6、正则化与岭回归


代码
# ---------使用岭回归预测------------- rg = Ridge(alpha=1.0) #alpha可以交叉验证调优 rg.fit(x_train, y_train) print(rg.coef_) # 计算出来的w值 y_rg_predict = s2.inverse_transform(rg.predict(x_test)) print("每个样本的预测价格:", y_rg_predict) print("岭回归的均方误差:", mean_squared_error(s2.inverse_transform(y_test),y_rg_predict))

7、总结
当样本数据量大时使用梯度下降,当数据量小时,比较岭回归和正规方程使用。
二、逻辑回归(解决二分类问题)
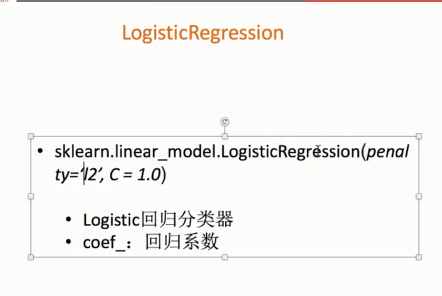
1、api

2、应用场景

3、公式

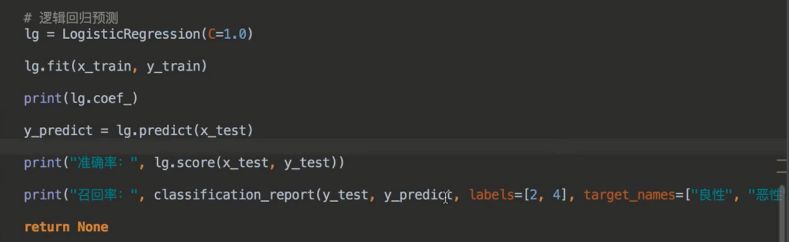
4、案例


5、总结
