题意:
小铭铭最近获得了一副新的桌游,游戏中需要用 mm 个骑士攻占 nn 个城池。
这 nn 个城池用 11 到 nn 的整数表示。除 11 号城池外,城池 ii 会受到另一座城池 fifi 的管辖,其中 fi<ifi<i。也就是说,所有城池构成了一棵有根树。这 mm 个骑士用 11 到 mm 的整数表示,其中第 ii 个骑士的初始战斗力为 sisi,第一个攻击的城池为 cici。
每个城池有一个防御值 hihi,如果一个骑士的战斗力大于等于城池的生命值,那么骑士就可以占领这座城池;否则占领失败,骑士将在这座城池牺牲。占领一个城池以后,骑士的战斗力将发生变化,然后继续攻击管辖这座城池的城池,直到占领 11 号城池,或牺牲为止。
除 11 号城池外,每个城池 ii 会给出两个战斗力变化参数 ai,viai,vi。若 ai=0ai=0,攻占城池 ii 以后骑士战斗力会增加 vivi;若 ai=1ai=1,攻占城池 ii 以后,战斗力会乘以 vivi。注意每个骑士是单独计算的。也就是说一个骑士攻击一座城池,不管结果如何,均不会影响其他骑士攻击这座城池的结果。
现在的问题是,对于每个城池,输出有多少个骑士在这里牺牲;对于每个骑士,输出他攻占的城池数量。
分析:
一开始想写倍增,结果发现数组开不开。
再重新考虑暴力的优化
一个一个人跳的话显然会同时走过很多重复的路径
所以可以用类似树上差分的思路,
从最底下的人开始往上跳,顺便带着上面的人一起走
那么就可以给每个点开一个小根堆记录当前点能活着的人
那么用小根堆显然是比较方便把失败的人弹出去
而且用左偏树还可以进行子节点向上合并的合并操作
但问题是每次往上跳
该小根堆的每个节点都要进行乘或加的操作也就是会被修改
而每次遍历所有节点修改其值显然还是会t
所以就要用类似线段树的方法打上乘和加的标记
如:打乘的标记:
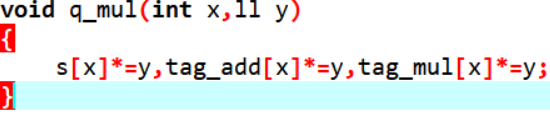
加的标记:

记得要先乘后加

然后merge部分与板子类似,不过选出当前根节点之前要先把标记下传,要不然标记会影响到新并进来的(显然)

因为题目中fi<i的,所以其实从底开始枚举时只需要从n->1枚举即可,求deep值时也只需要从1->n 遍历一遍即可,不需要dfs
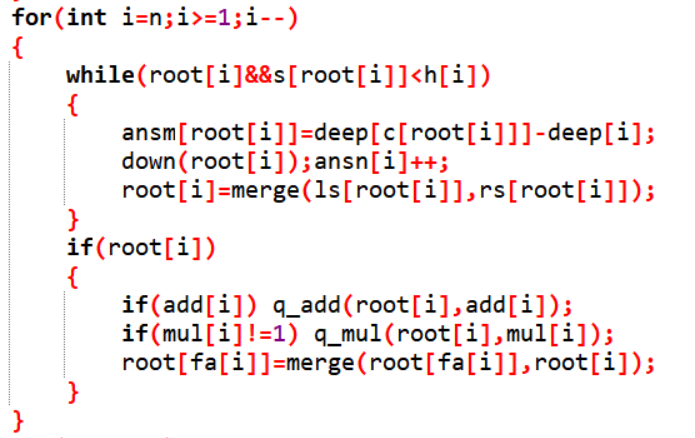

如果有人一路打到通关,那我们就把它挂在0号节点上,没通关的人结果提前就能求出来
通关并挂在0节点上的人结果就是deep值,因为显然他通关了一定打过deep个城池
代码:
#include<cstdio> #include<algorithm> using namespace std; #define ll long long const int maxn=3e5+1; int fa[maxn]; int c[maxn]; int ansn[maxn]; int ansm[maxn]; int deep[maxn]; int root[maxn]; int dis[maxn]; int ls[maxn]; int rs[maxn]; ll h[maxn]; ll mul[maxn]; ll add[maxn]; ll s[maxn]; ll tag_mul[maxn]; ll tag_add[maxn]; void q_add(int x,ll y) { s[x]+=y,tag_add[x]+=y; } void q_mul(int x,ll y) { s[x]*=y,tag_add[x]*=y,tag_mul[x]*=y; } void down(int x) { if(tag_mul[x]!=1) { if(ls[x]) q_mul(ls[x],tag_mul[x]); if(rs[x]) q_mul(rs[x],tag_mul[x]); tag_mul[x]=1; } if(tag_add[x]) { if(ls[x]) q_add(ls[x],tag_add[x]); if(rs[x]) q_add(rs[x],tag_add[x]); tag_add[x]=0; } } int merge(int x,int y) { if(!x||!y) return x+y; if(s[x]>s[y]) swap(x,y); down(x),rs[x]=merge(rs[x],y); if(dis[ls[x]]<dis[rs[x]]) swap(ls[x],rs[x]); dis[x]=dis[rs[x]]+1; return x; } void dfs(int x) { ansm[x]=deep[c[x]]; if(ls[x]) dfs(ls[x]); if(rs[x]) dfs(rs[x]); } int main() { int n,m,p; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) scanf("%lld",&h[i]); for(int i=2;i<=n;i++) { scanf("%d%d",&fa[i],&p); if(p) scanf("%lld",&mul[i]),add[i]=0; else scanf("%lld",&add[i]),mul[i]=1; } for(int i=1;i<=n;i++) deep[i]=deep[fa[i]]+1; for(int i=1;i<=m;i++) tag_mul[i]=1; for(int i=1;i<=m;i++) { scanf("%lld%d",&s[i],&c[i]); root[c[i]]=merge(root[c[i]],i); } for(int i=n;i>=1;i--) { while(root[i]&&s[root[i]]<h[i]) { ansm[root[i]]=deep[c[root[i]]]-deep[i]; down(root[i]);ansn[i]++; root[i]=merge(ls[root[i]],rs[root[i]]); } if(root[i]) { if(add[i]) q_add(root[i],add[i]); if(mul[i]!=1) q_mul(root[i],mul[i]); root[fa[i]]=merge(root[fa[i]],root[i]); } } dfs(root[0]); for(int i=1;i<=n;i++) printf("%d ",ansn[i]); for(int i=1;i<=m;i++) printf("%d ",ansm[i]); return 0; }