图的存储结构:1. 邻接矩阵表示法 2. 邻接表表示法
邻接矩阵表示法(数组表示法):适用稠密图
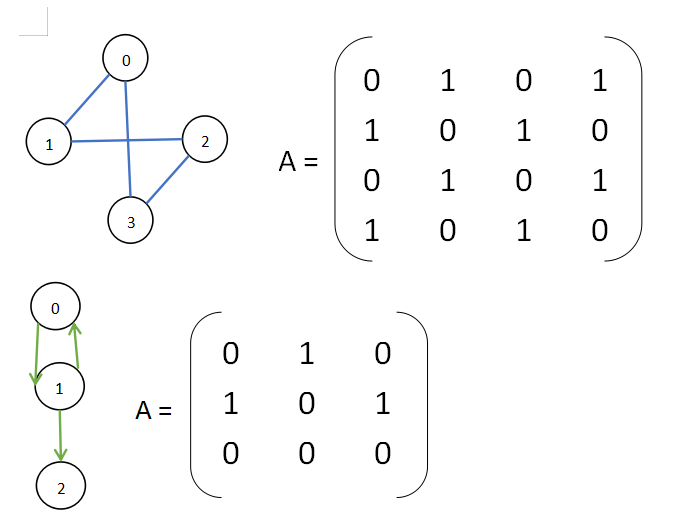
无向图的邻接矩阵是对称的;
有向图的邻接矩阵可能是不对称的。
在有向图中,(出行入列)
第 i 行 1 的个数 = 顶点 i 的出度;
第 j 列 1 的个数 = 顶点 j 的入度。
在无向图中,
第 i 行(列)1 的个数 = 顶点 i 的度
邻接表表示法:适用稀疏图
无向图的邻接表:
有向图的邻接表有:邻接表(出边表);逆邻接表(入边表)。
图的遍历:深度优先搜索 DFS;广度优先搜索 BFS
深度优先搜索 DFS: (递归过程,类似于先序遍历。非递归的可借助栈实现)
(1)从图中某个顶点 v0出发,首先访问 v0。
(2)找出 v0 的第一个未被访问的邻接点 v1,然后访问 v1。以 v1为新顶点,重复此步骤,直到刚访问过的顶点没有未被访问的邻接点为止。
(3)返回前一个访问过的且仍有未被访问的邻接点的顶点,找出该顶点的下一个未被访问的邻接点,访问该顶点,然后执行步骤(2)。
广度优先搜索 BFS:(可借助队列实现,类似于层序遍历)
(1)从图中某个顶点 v0出发,首先访问 v0。
(2)依次访问 v0的各个未被访问的邻接点。
(3)分别从这些邻接点出发,依次访问它们的各个未被访问的邻接点。
(4)重复(3),直到所有顶点均没有未被访问的邻接点为止。
访问时应保证:如果 vi和 vk为当前顶点,且 vi在 vk之前被访问,则 vi的所有未被访问的邻接点应在 vk的所有未被访问的邻接点之前访问。
克鲁斯卡尔算法适合求(边稀疏连通网)的最小生成树
具有 n 个顶点的图其生成树有且仅有 n-1 条边。