图的基本概念及基本术语
Graph=(V,R)
V 是顶点的非空有限集;R 是边的有限集,可为空集
简单分类:
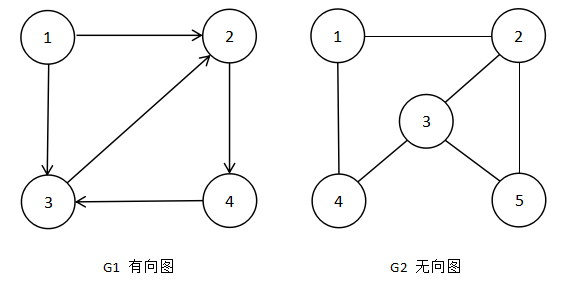
有向图 G1={V,R}
V(G1)={1,2,3,4}
R(G1)={<1,2>,<1,3>,<2,4>,<3,2>,<4,3>}
无向图 G2={V,R}
V(G2)={1,2,3,4}
R(G2)={(1,2),(1,4),(2,3),(2,5),(3,4),(3,5)}
有n个顶点的无向图最多有 n*(n - 1)/ 2 条边。
有n个顶点的有向图最多有 n*(n - 1) 条边。
完全图:设|V|=n,|E|=e
(1)对有向图G,若e=n(n-1),则称G为完全有向图;
(2)对无向图G,若e=n(n-1)/2,则称G为完全无向图;
赋权图:
若【无 / 有】向图的每条边都带一个权,则称相应的图为 赋权【无 / 有】向图。
权是具有某种实际意义的数,如:2个顶点之间的距离,耗费等。
网:带权的图称为赋权图或网。
邻接点、关联
(1)若(u,v)是一条无向边,则称 u和v互为邻接点,称 边(u,v)与两个顶点互相关联。
(2)若<u,v>是一条有向边,则称 顶点u邻接到顶点v;顶点v邻接自顶点u,称 弧<u,v>与顶点u和v互相关联。
顶点的度
无向图顶点的度:
关联于该顶点的边的数目,记为D(v)。
有向图顶点: 在有 n 个顶点的有向图中,每个顶点的度最大可达 2(n-1)。
(1)以顶点v为终点的边的数目,称为v的入度,记为ID(v)
(2)以顶点v为起点的边的数目,称为v的出度,记为OD(v)
(3)顶点v的度则定义为该顶点的入度与出度之和,即 D(v)=ID(v)+OD(v)
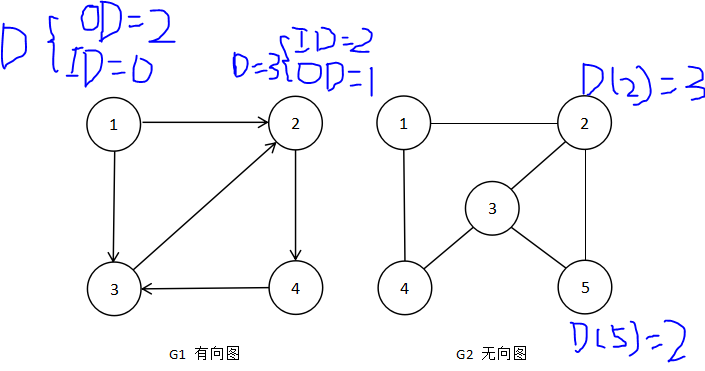
规律1:边数和结点度数的关系
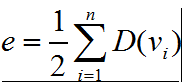 度数是边数的2倍
度数是边数的2倍
规律2:有向图,所有顶点的入度之和
= 所有顶点的出度之和
= 弧数
路径、路径长度
在无向图G中,以上面的图例为例,存在顶点序列{1,2,3,4,5},
顶点1到顶点3可以是:(1,2,3);(1,2,5,3) ,这就是顶点1和顶点3之间的路径
路径所包含的边(弧)数称为该路径的长度,比如(1,2,5,3)这条路径的长度就是3。
简单路:
若一条路径上除了起点和终点可能相同外,其余顶点均不相同,则称此路径为一条简单路径。
回路:
起点和终点相同的路径称为回路 / 环 / 圈
起点和终点相同的简单路径称为简单回路 / 简单环 / 简单圈
连通图(无向图):具有 n 个顶点的无向图至少应有 n-1 条边才能确保是一个连通图
在无向图G中,若从顶点u到顶点v有一条路径,则称顶点u和v在图G中是连通的。
若V(G)中任意2个不同的顶点u和v都是连通的,则称G为连通图。
强连通图(有向图):
在有向图G中,若对于V(G)中任意2个不同的顶点u和v,都存在从u到v以及从v到u的路径,则称G为强连通图。
连通分支(无向图):
任何连通图只有一个连通分支,即其自身。而非连通的无向图有多个连通分支。
强连通分支(有向图):
强连通图只有一个强连通分支,即其自身。非强连通的有向图有多个强连通分支。
Graph 图;Vertex 顶点;Arc 弧
图的基本操作:
-
CreateGraph(G):创建图G
-
DestroyGraph(G):销毁图G
-
LocateVertex(G,v):返回顶点 v 在图G中的位置,若没有顶点v,则返回值为“空”(-1)
-
GetVertex(G,i):返回图G中第 i 个顶点的值,若 i 大于图G中顶点数,则返回值为“空”(-1)
-
FirstAdjVertex(G,v):图G中顶点 v 的第一个邻接点。若 v 无邻接点或图G中无顶点 v ,则返回值为"空" (-1)
-
NextAdjVertex(G,v,w):图G中顶点 v 的下一个邻接点(紧跟在 w 后面) 。 若 w 是 v 的最后一个邻接点,则函数返回值为"空"。
-
InsertVertex(G,u):在图G中增加一个顶点 u 。
-
Delete Vertex(G,v):删除图G中顶点 v 及与顶点 v 相关联的弧(边)。
-
InsertArc(G,v,w):在图G中增加一条从顶点 v 到顶点 w 的弧。
-
DeleteArc(G,v,w):删除图G中从顶点 v 到顶点 w 的弧(边)。
-
TraverseGraph(G):对图G的每个顶点访问一次且仅访问一次。