
定义4 设A=(aij) 是一个m×s矩阵,B=(bij) 是一个s×n矩阵,那么规定矩 阵 A 与矩阵 B 的乘积是一个 m×n 矩阵 C =(cij),
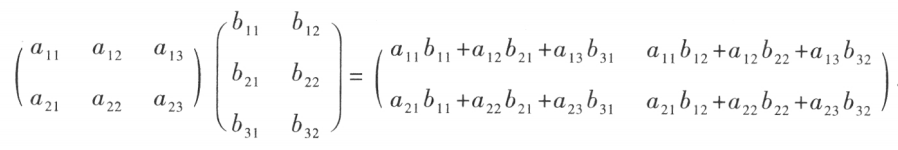
并把此乘积记作 C = A B
矩阵的乘法不满足交换律,即在一般情形下,A B≠BA
矩阵的乘法虽不满足交换律,但仍满足下列结合律和分配律(假设运算都 是可行的):
(i)(A B)C = A(B C);
(ii)λ(A B)=(λA)B = A(λB)(其中λ为数);
(iii) A(B + C)= A B +A C,(B + C)A = BA + CA
对于单位矩阵 E,容易验证 E m A m ×n = A m ×n, A m ×n E n = A m × n,
或简写成 E A = A E = A
由于矩阵乘法适合结合律,所以矩阵的幂满足以下运算规律: A k A l = A k+l,(A k)l = A kl,
矩阵乘法一般不满足交换律,所以对于两个 n 阶矩阵 A 与 B,一般说来(A B)k≠A k B k,只有当 A 与 B 可交换时,才有(A B)k = A k B k
类似 可知,例如(A +B)2 = A 2 +2A B + B 2、(A - B)(A + B)= A 2 - B 2 等公式,也只有当 A 与 B 可交换时才成立.
