后缀数组（模板）

介绍

后缀数组就是字符串的每个后缀的排序。
主要有两个sa和rk两个数组，sa[i]代表第i大的后缀的位置，rk[i]代表位置i的后缀的排位。满足rk[sa[i]] = sa[rk[i]] = i

实现

有很多求后缀数组的方法，其中一种是倍增法。
先给字符串每一位排序，然后倍增排序。假设当前倍增长度为(2^k)，那么对于位置i，以rk[i]为第一关键字，rk[i+(2^k)]为第二关键字排序。
时间复杂度O(n(logn)^2)。

偷个oiwiki的图，倍增排序示意图：

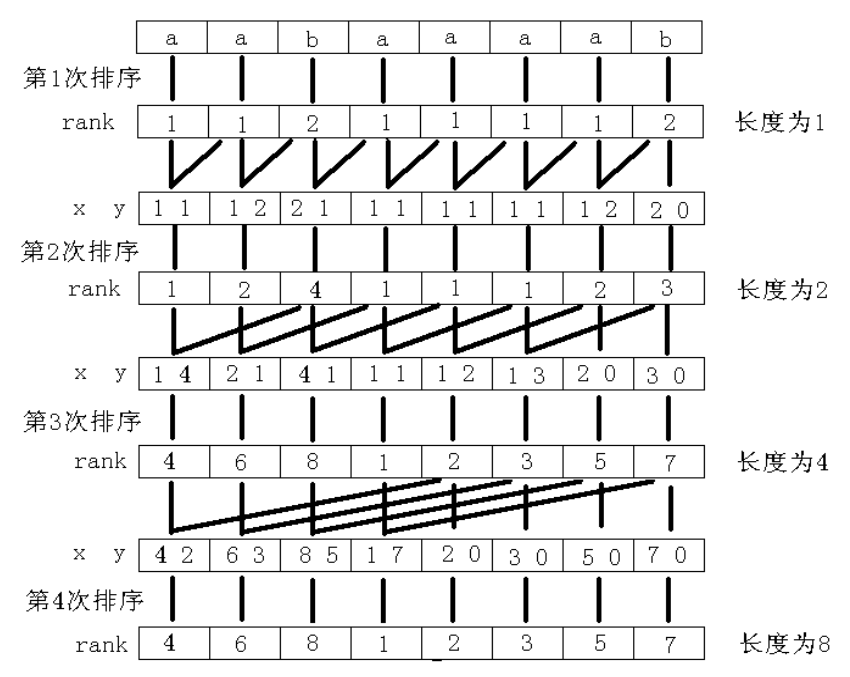
还有O(n)的复杂度的方法，有机会再补了。

const int N = 2e6 + 10;
typedef long long ll;
//倍增要开两倍空间，每次排序的格式化也要格式化两倍空间（重要）
// 字符串下标从 0 开始；sa、rk从 1 开始
int sa[N], pos[N], rk[N << 1], oldrk[N << 1]; 
char s[N];

void solve(char s[]) {
    int n = strlen(s);
    for(int i = 0; i < n; i++) {
        pos[i + 1] = i;
        cnt[i] = sa[i] = rk[i] = rk[i + n] = ht[i] = 0;
    }
    sort(pos + 1, pos + 1 + n, [s](int x, int y) {return s[x] < s[y];});
    int rnk = 1;
    for(int i = 1; i <= n; i++) {
        if(i > 1 && s[pos[i]] > s[pos[i - 1]]) rnk++;
        rk[pos[i] + 1] = rnk;
    }
    for(int w = 1; w < n; w <<= 1) {
        for(int i = 1; i <= n; i++) sa[i] = i;
        sort(sa + 1, sa + n + 1, [w](int x, int y) {return rk[x] == rk[y] ? rk[x + w] < rk[y + w] : rk[x] < rk[y];});
        for(int i = 0; i <= (n << 1); i++) oldrk[i] = rk[i]; //两倍空间，拷贝要完整地拷贝
        int p = 0;
        for(int i = 1; i <= n; i++) {
            if(oldrk[sa[i]] == oldrk[sa[i - 1]] && oldrk[sa[i] + w] == oldrk[sa[i - 1] + w]) {
                rk[sa[i]] = p;
            } else {
                rk[sa[i]] = ++p;
            }
        }
    }
    
    // 注意这里s下标从0开始，while内部要减1
    int k = 0;
    for(int i = 1; i <= n; i++) {
        if(k) k--;
        while(i + k < n && s[i + k - 1] == s[sa[rk[i] - 1] + k - 1]) k++;
        ht[rk[i]] = k;
    }

}

// rk、sa从1开始
// px[i] = rk[id[i]]（用于排序的数组所以叫 px）
const int N = 1e6 + 10;
int n, sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N], pos[N], ht[N];
char s[N];

bool cmp(int x, int y, int w) {
  return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}

void solve(char s[]) {
    int n = strlen(s);
    for(int i = 0; i < n; i++) pos[i + 1] = i;
    sort(pos + 1, pos + 1 + n, [s](int x, int y) {return s[x] < s[y];});
    int rnk = 1;
    for(int i = 1; i <= n; i++) {
        if(i > 1 && s[pos[i]] > s[pos[i - 1]]) rnk++;
        rk[pos[i] + 1] = rnk;
    }
    int m = n, p; // m为值域，可以改小
    for(int i = 1; i <= m; i++) cnt[i] = 0;
    for(int i = 1; i <= n; i++) ++cnt[rk[i]];
    for(int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];
    for(int i = n; i >= 1; i--) sa[cnt[rk[i]]--] = i;
    // m=p 就是优化计数排序值域
    for(int w = 1;;w <<= 1, m = p) {
        p = 0;
        for(int i = n; i > n - w; --i) id[++p] = i;
        for(int i = 1; i <= n; ++i)
            if(sa[i] > w) id[++p] = sa[i] - w;
        for(int i = 1; i <= m; i++) cnt[i] = 0;
        for(int i = 1; i <= n; i++) ++cnt[px[i] = rk[id[i]]];
        for(int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];
        for(int i = n; i >= 1; i--) sa[cnt[px[i]]--] = id[i];
        for(int i = 1; i <= (n << 1); i++) oldrk[i] = rk[i];
        p = 0;
        for(int i = 1; i <= n; i++)
            rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
        if(p == n) {
            for(int i = 1; i <= n; i++) sa[rk[i]] = i;
            break;
        }
    }
}

height数组

(height[i] = lcp(sa[i], sa[i-1])), 即第i名的后缀与它前一名的后缀的最长公共前缀。

具体就是使用引理(height[rk[i]] le height[rk[i-1]]-1)来暴力求，时间复杂度O(n)。

// 注意这里s下标从0开始，while内部要减1
int k = 0;
for(int i = 1; i <= n; i++) {
    if(k) k--;
    while(i + k < n && s[i + k - 1] == s[sa[rk[i] - 1] + k - 1]) k++;
    ht[rk[i]] = k;
}

参考