Description
题目大意:将边长为1的 2n边形(n为奇数) 嵌入一个正方形。这个正方形的最小边长是多少?
思路
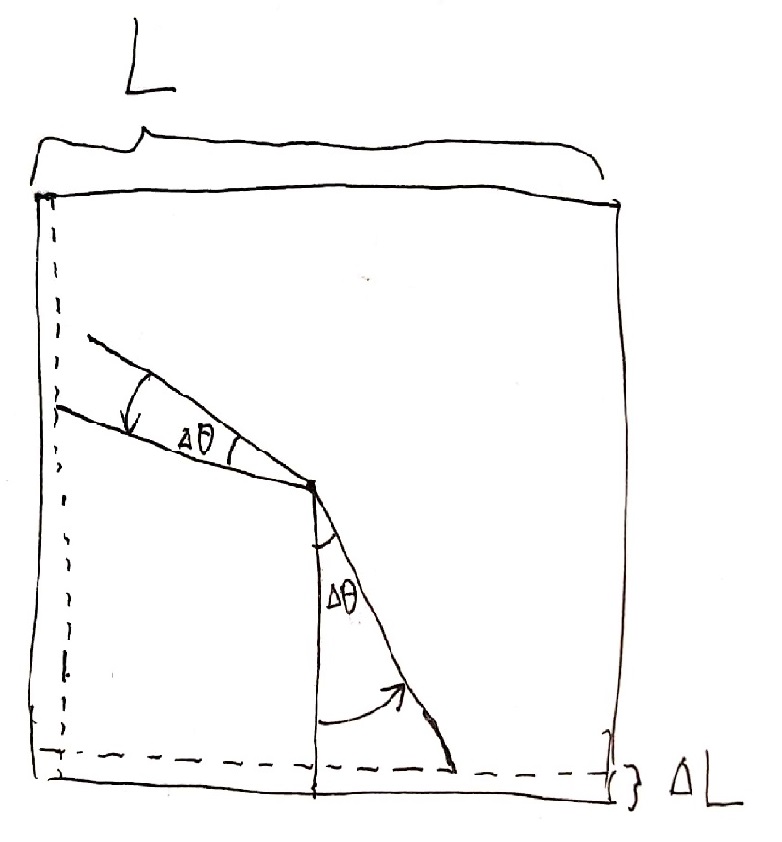
大体思路是二分边缩短((Delta L))的长度,判断多边形能否通过旋转塞进正方形当中(就是判断左上角的边会不会超出边界)。
只要图中那两条边放得进正方形,那么这两条边对应的多边形也放的进正方形。
#include <iostream>
#include <cstdio>
#include <queue>
#include <algorithm>
#include <map>
#include <set>
#include <vector>
#include <cstring>
#include <string>
#include <deque>
#include <cmath>
#include <iomanip>
#include <cctype>
#define endl '
'
#define IOS std::ios::sync_with_stdio(0);
#define FILE freopen("..//data_generator//in.txt","r",stdin),freopen("res.txt","w",stdout)
#define FI freopen("..//data_generator//in.txt","r",stdin)
#define FO freopen("res.txt","w",stdout)
#define md make_pair
#define pb push_back
#define mp make_pair
#define seteps(N) fixed << setprecision(N)
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
inline ll qmul(ll a, ll b, ll m) {
ll res = 0;
while(b) {
if(b & 1) res = (res + a) % m;
a = (a << 1) % m;
b = b >> 1;
}
return res;
}
inline ll qpow(ll a, ll b, ll m) {
ll res = 1;
while(b) {
if(b & 1) res = (res * a) % m;
a = (a * a) % m;
b = b >> 1;
}
return res;
}
inline ll inv(ll x, ll q) {
return qpow(x, q - 2, q);
}
using namespace std;
/*-----------------------------------------------------------------*/
#define INF 0x3f3f3f3f
const int N = 3e6 + 10;
const double eps = 1e-10;
char s[N];
const long double PI = 3.14159265358979323846;
int main() {
IOS;
int t;
cin >> t;
while(t--) {
int n;
cin >> n;
long double o = PI / n;
long double L = (long double)0.5 / sin(o / 2);
long double l = 0, r = L - cos(o / 2) * L;
while(r - l > eps) {
long double deL = (l + r) / 2;
long double deo = acos((L - deL) / L);
if(L * cos(o / 2 - deo) <= L - deL) l = deL;
else r = deL;
}
cout << seteps(10) << 2 * (L - l) << endl;
}
}