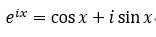一. 分解质因数
每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,把一个合数用质因数相乘的形式表示出来,叫做分解质因数。如30=2×3×5 。分解质因数只针对合数。求一个数的质因数,要从最小的质数除起,一直除到结果为质数为止。分解质因数的算式叫短除法,和除法的性质相似,还可以用来求多个数的公因式。(百科)
const int MAXN = 100010;
int prime[MAXN] = {0};
bool isprime[MAXN] = {0};
int id = 0;
void getPrime() //素数筛法
{
for (int i = 2; i < MAXN; i++)
{
if (!isprime[i])
prime[id++] = i;
for (int j = 0; j < id && i * prime[j] <= MAXN && i * prime[j] != 0; j++)
isprime[i * prime[j]] = 1;
}
}
void getPrimeFactor(int n) //分解质因数,递归输出素因子
{
getPrime();
if (n < 2)
return;
if (!isprime[n])
cout << n;
else
{
for (int i = 0; prime[i] < n; i++)
if (n % prime[i] == 0)
{
cout << prime[i] << " ";
getPrimeFactor(n / prime[i]);
break;
}
}
}
二. 欧拉函数
对正整数n,欧拉函数是小于或等于n的正整数中与n互质的数的数目。根据定义可以写出
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int getfi(int n)
{
int fi = 0;
for (int i = 1; i < n; i++)
if (gcd(i, n) == 1)
fi++;
return fi;
}
根据欧拉函数通式
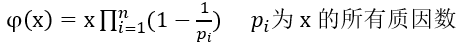
可以写出
int ksm(int a, int b)//快速幂
{
int res = 1;
for (; b; b >>= 1, a *= a)
if (b & 1)
res *= a;
return res;
}
int getfi(int n)
{
int fi = 1;
getPrime();
if (n == 1 || !isprime[n])
return 1;
for (int i = 0; prime[i] < n; i++)
if (n % prime[i] == 0)
{
int cnt = 0;
while (n % prime[i] == 0)
{
cnt++;
n /= prime[i];
}
fi *= (prime[i] - 1) * ksm(prime[i], cnt - 1);
}
return fi;
}
欧拉函数通式可根据算数基本定理证明:
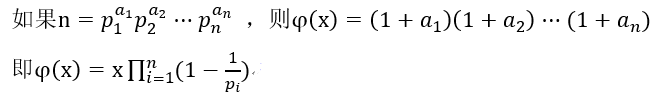
三. 欧拉定理
欧拉定理描述:
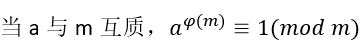
扩展欧拉定理:
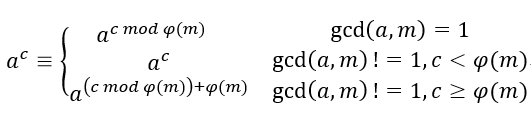
Super_log 题目链接: https://nanti.jisuanke.com/t/41299
题目大意是已知a,b,m,1≤a≤1000000,0≤b≤1000000,1≤m≤1000000
求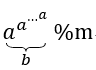
类似的,我们可以欧拉降幂

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 ll ksm(ll a, ll b, ll mod) 5 { 6 ll res = 1; 7 for (; b; b >>= 1, a = a * a % mod) 8 if (b & 1) 9 res = res * a % mod; 10 return res; 11 } 12 ll getfi(ll x) 13 { 14 ll i, ans = x; 15 for (i = 2; i * i <= x; i++) 16 { 17 if (x % i == 0) 18 { 19 ans = ans / i * (i - 1); 20 while (x % i == 0) 21 x /= i; 22 } 23 } 24 if (x != 1) 25 ans = ans / x * (x - 1); 26 return ans; 27 } 28 ll solve(ll n, ll m, ll p) 29 { 30 if (p == 1) 31 return 0; 32 if (m == 0) 33 return 1; 34 ll fi = getfi(p); 35 ll f = solve(n, m - 1, fi); 36 if (f < fi && f) 37 return ksm(n, f, p); 38 else 39 return ksm(n, f + fi, p); 40 } 41 int main() 42 { 43 int t; 44 cin >> t; 45 while (t--) 46 { 47 ll a, b, m; 48 cin >> a >> b >> m; 49 ll ans = solve(a, b, m); 50 cout << ans % m << endl; 51 } 52 return 0; 53 }
ps:欧拉公式:
跟上述无关,纯粹为了区分