一、问题描述
矩阵乘法规则
如果A是a*b的矩阵,B是b*c的矩阵,那么AB就是a*c的矩阵,所做的乘法次数为a*b*c
矩阵链乘法
给定一个矩阵链A1A2A3A4,要计算乘积,给这个矩阵链加上括号,来改变运算次序。
如果矩阵链为(A1,A2,A3,A4),那么有如下5中加括号的方式:
(A1(A2(A3A4)))
(A1((A2A3)A4))
((A1A2)(A3A4))
((A1(A2A3))A4)
(((A1A2)A3)A4)
而改变矩阵的运算次序,能改变所做乘法的运算次数,比如说3个矩阵的链(A1,A2,A3),假设3个矩阵的维数分别为10*100,100*5,5*50。按照((A1,A2)A3)的次序来计算,需要10*100*5+10*5*50=7500次乘法。但如果按照(A1(A2,A3))的次序来计算,则需要100*5*50+10*100*50=75000次乘法,慢了10倍。
总而言之,矩阵链中不同的运算顺序会导致运算次数有很大的差异
矩阵链乘法问题
矩阵链乘法问题就是寻找一个最佳的运算次序,使所做的乘法次数最小
p[n+1]:表示n个矩阵的维度,其中矩阵Ai的维度为pi-1*pi
二、问题分析
由前面可知,一个序列如果只有一个矩阵,则只有一种方式加全部括号,如果有两个或两个以上的矩阵,则必然可以看做两个子序列的乘积,且这两个子序列又可以分解成更小的两个子序列的乘积(两个矩阵相乘的运算次数看前面)。我们用cost(i,j)表示序列Ai…Aj在最优加全部括号时的标量乘积次数,则
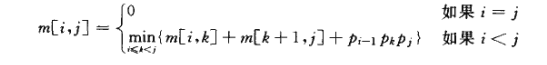
其中pi-1pk pj为子序列Ai…Ak与Ak+1…Aj相乘时的标量相乘次数。
三、代码实现
代码中,测试用例为6个矩阵相乘,各个矩阵的维度存放在p中
int main()
{
//代表矩阵链
int p[7] = {30,35,15,5,10,20,25};
//mij表示矩阵i到矩阵j的最小代价
int m[7][7] = {0};
//sij表示矩阵i到矩阵j最小代价的分割点
int s[7][7];
//长度为1的矩阵代价设为0
for (int i = 1; i <= 6; i++)
m[i][i] = 0;
//对于每一个大于1的长度
for (int j = 2; j <= 6; j++)
//k为左端点位置,取值不能大于6-k+1,这是计算位置的方式,要记得,
for (int k = 1; k <= 6 - j + 1; k++) {
int end = k + j - 1;//end为右端点位置
m[k][end] = 999999;
//计算代价,图个代价等于划分位置两边的矩阵代价,加上两矩阵合并代价
for (int n = k; n <= end; n++) {
int temp = m[k][n] + m[n + 1][end] + p[k-1] * p[n] * p[end];
if (temp < m[k][end]) {
m[k][end] = temp;
s[k][end] = n;
}
}
}
cout << m[1][6] << endl;
system("pause");
return 0;
}
最终输出结果为15125,表示最优运算次数。