迪杰斯特拉(di jie qi)算法
这里有一张图:
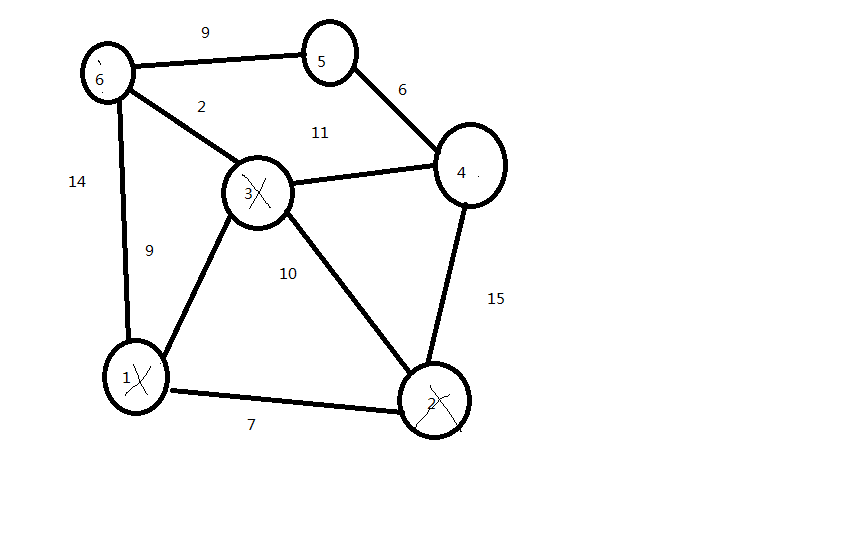
假设要求从1号节点到5号节点的最短路。那么根据迪杰斯特拉算法的思想,我们先看:
节点1,从节点1出发的一共有3条路,分别是1-6、1-3、1-2。然后我们分别看每条路的权值,发现1-6的权值为14,记录下来、1-3的权值为9,记录下来、1-2的权值为7,记录下来。我们发现好像不能再从1号节点发现什么了,所以,我们把它out掉。
接着按顺序看2号节点,从节点2发出了2条路分别是2-3与2-4,我们接着向计算1号节点一样计算2号节点。先计算2-3,权值为10。咦?我们好像已经在计算1号节点的时候标记过了,也就是说现在到3号节点有两种方案,分别是1-3与1-2-3,通过比较,我们发现9〉7+10,所以标记不变,依旧是9。接下来看2-4,没有被标记过,记录15。Out掉节点2
然后就该节点3了,我们发现有两条路,且都没被标记过,分别记录2与11,out掉节点3
节点4有两条路,发现从3-4更方便标记11。Out掉。
节点6有两条路,3-6方便标记为2。Out掉。
最后5号节点有两条路从4到5最短,5号节点标记为6。
我们达到了光辉的顶点,发现最后路径是1-3-6-5和为20。
迪杰斯特拉算法具有明显的贪心特征,通过每个节点去最优值的过程我们称之为“松弛”,松弛之后,答案显而易见。
实际上对于松弛过程的模拟,核心代码只有两行:
if(dis[v]>dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
(咦,你的核心代码为什么没有找最近的节点?哈哈思(sheng)考(lve))
迪杰斯特拉算法的局限性
不难看出(好粗暴的词汇)它的时间复杂度为O((M+N)logN)空间复杂度为O(M)看起来还不错,但它无法解决权值为负数的情况,所以用前先审题哦。