深入解析最小生成树
正文
所谓最小生成树,就是在一个具有N个顶点的带权连通图G中,如果存在某个子图G',其包含了图G中的所有顶点和一部分边,且不形成回路,并且子图G'的各边权值之和最小,则称G'为图G的最小生成树。
由定义我们可得知最小生成树的三个性质:
•最小生成树不能有回路。
•最小生成树可能是一个,也可能是多个。
•最小生成树边的个数等于顶点的个数减一。
本文将介绍两种最小生成树的算法,分别为克鲁斯卡尔算法(Kruskal Algorithm)和普利姆算法(Prim Algorithm)。
第一节 克鲁斯卡尔算法(Kruskal Algorithm)
克鲁斯卡尔算法的核心思想是:在带权连通图中,不断地在边集合中找到最小的边,如果该边满足得到最小生成树的条件,就将其构造,直到最后得到一颗最小生成树。
克鲁斯卡尔算法的执行步骤:
第一步:在带权连通图中,将边的权值排序;
第二步:判断是否需要选择这条边(此时图中的边已按权值从小到大排好序)。判断的依据是边的两个顶点是否已连通,如果连通则继续下一条;如果不连通,那么就选择使其连通。
第三步:循环第二步,直到图中所有的顶点都在同一个连通分量中,即得到最小生成树。
下面我用图示法来演示克鲁斯卡尔算法的工作流程,如下图:
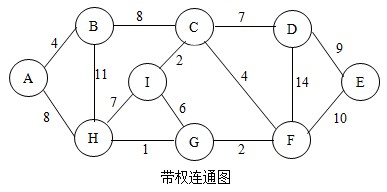
所谓最小生成树,就是在一个具有N个顶点的带权连通图G中,如果存在某个子图G',其包含了图G中的所有顶点和一部分边,且不形成回路,并且子图G'的各边权值之和最小,则称G'为图G的最小生成树。
由定义我们可得知最小生成树的三个性质:
•最小生成树不能有回路。
•最小生成树可能是一个,也可能是多个。
•最小生成树边的个数等于顶点的个数减一。
本文将介绍两种最小生成树的算法,分别为克鲁斯卡尔算法(Kruskal Algorithm)和普利姆算法(Prim Algorithm)。
第一节 克鲁斯卡尔算法(Kruskal Algorithm)
克鲁斯卡尔算法的核心思想是:在带权连通图中,不断地在边集合中找到最小的边,如果该边满足得到最小生成树的条件,就将其构造,直到最后得到一颗最小生成树。
克鲁斯卡尔算法的执行步骤:
第一步:在带权连通图中,将边的权值排序;
第二步:判断是否需要选择这条边(此时图中的边已按权值从小到大排好序)。判断的依据是边的两个顶点是否已连通,如果连通则继续下一条;如果不连通,那么就选择使其连通。
第三步:循环第二步,直到图中所有的顶点都在同一个连通分量中,即得到最小生成树。
下面我用图示法来演示克鲁斯卡尔算法的工作流程,如下图:

首先,将图中所有的边排序(从小到大),我们将以此结果来选择。排序后各边按权值从小到大依次是:
HG < (CI=GF) < (AB=CF) < GI < (CD=HI) < (AH=BC) < DE < BH < DF
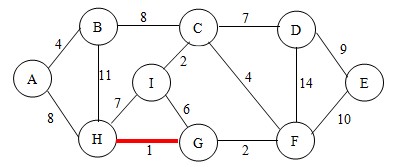
接下来,我们先选择HG边,将这两个点加入到已找到点的集合。这样图就变成了,如图

继续,这次选择边CI(当有两条边权值相等时,可随意选一条),此时需做判断。
判断法则:当将边CI加入到已找到边的集合中时,是否会形成回路?
1.如果没有形成回路,那么直接将其连通。此时,对于边的集合又要做一次判断:这两个点是否在已找到点的集合中出现过?
①.如果两个点都没有出现过,那么将这两个点都加入已找到点的集合中;
②.如果其中一个点在集合中出现过,那么将另一个没有出现过的点加入到集合中;
③.如果这两个点都出现过,则不用加入到集合中。
2.如果形成回路,不符合要求,直接进行下一次操作。
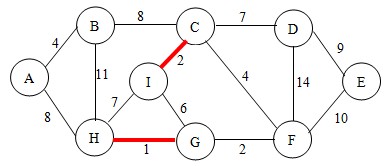
根据判断法则,不会形成回路,将点C和点I连通,并将点C和点I加入到集合中。如图:
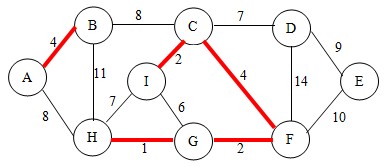
 继续,这次选择边GF,根据判断法则,不会形成回路,将点G和点F连通,并将点F加入到集合中。如图:
继续,这次选择边GF,根据判断法则,不会形成回路,将点G和点F连通,并将点F加入到集合中。如图:
 继续,这次选择边AB,根据判断法则,不会形成回路,将其连通,并将点A和点B加入到集合中。如图:
继续,这次选择边AB,根据判断法则,不会形成回路,将其连通,并将点A和点B加入到集合中。如图:
 继续,这次选择边CF,根据判断法则,不会形成回路,将其连通,此时这两个点已经在集合中了,所以不用加入。如图:
继续,这次选择边CF,根据判断法则,不会形成回路,将其连通,此时这两个点已经在集合中了,所以不用加入。如图:
 继续,这次选择边GI,根据判断法则,会形成回路,如下图,直接进行下一次操作。
继续,这次选择边GI,根据判断法则,会形成回路,如下图,直接进行下一次操作。
 继续,这次选择边CD,根据判断法则,不会形成回路,将其连通,并将点D加入到集合中。如图:
继续,这次选择边CD,根据判断法则,不会形成回路,将其连通,并将点D加入到集合中。如图:
 继续,这次选择边HI,根据判断法则,会形成回路,直接进行下一次操作。
继续,这次选择边HI,根据判断法则,会形成回路,直接进行下一次操作。
继续,这次选择边AH,根据判断法则,不会形成回路,将其连通,此时这两个点已经在集合中了,所以不用加入。
继续,这次选择边BC,根据判断法则,会形成回路,直接进行下一次操作。
继续,这次选择边DE,根据判断法则,不会形成回路,将其连通,并将点E加入到集合中。如图:
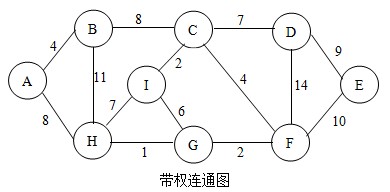
 继续,这次选择边BH,根据法则,会形成回路,进行下一次操作。
继续,这次选择边BH,根据法则,会形成回路,进行下一次操作。
最后选择边DF,根据法则,会形成回路,不将其连通,也不用加入到集合中。
好了,所有的边都遍历完成了,所有的顶点都在同一个连通分量中,我们得到了这颗最小生成树。
通过生成的过程可以看出,能否得到最小生成树的核心问题就是上面所描述的判断法则。那么,我们如何用算法来描述判断法则呢?我认为只需要三个步骤即可:
⒈将某次操作选择的边XY的两个顶点X和Y和已找到点的集合作比较,如果
①.这两个点都在已找到点的集合中,那么return 2;
②.这两个点有一个在已找到点的集合中,那么return 1;
③这两个点都不在一找到点的集合中,那么return 0;
⒉当返回值为0或1时,可判定不会形成回路;
⒊当返回值为2时,判定能形成回路的依据是:假如能形成回路,设能形成回路的点的集合中有A,B,C,D四个点,那么以点A为起始点,绕环路一周后必能回到点A。如果能回到,则形成回路;如果不能,则不能形成回路。
判定算法很清楚了,我们来写一下克鲁斯卡尔的核心算法,算法代码如下:
OK,克鲁斯卡尔算法介绍完了。
第二节 普利姆算法(Prim Algorithm)
普利姆算法的核心步骤是:在带权连通图中,从图中某一顶点v开始,此时集合U={v},重复执行下述操作:在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边,将(u,w)这条边加入到已找到边的集合,并且将点w加入到集合U中,当U=V时,就找到了这颗最小生成树。
其实,由步骤我们就可以定义查找法则:在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边。
ok,知道了普利姆算法的核心步骤,下面我就用图示法来演示一下工作流程,如图:
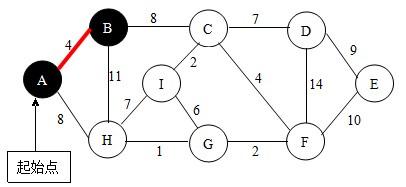
 首先,确定起始顶点。我以顶点A作为起始点。根据查找法则,与点A相邻的点有点B和点H,比较AB与AH,我们选择点B,如下图。并将点B加入到U中。
首先,确定起始顶点。我以顶点A作为起始点。根据查找法则,与点A相邻的点有点B和点H,比较AB与AH,我们选择点B,如下图。并将点B加入到U中。
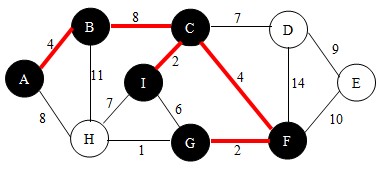
 继续下一步,此时集合U中有{A,B}两个点,再分别以这两点为起始点,根据查找法则,找到边BC(当有多条边权值相等时,可选任意一条),如下图。并将点C加入到U中。
继续下一步,此时集合U中有{A,B}两个点,再分别以这两点为起始点,根据查找法则,找到边BC(当有多条边权值相等时,可选任意一条),如下图。并将点C加入到U中。
 继续,此时集合U中有{A,B,C}三个点,根据查找法则,我们找到了符合要求的边CI,如下图。并将点I加入到U中。
继续,此时集合U中有{A,B,C}三个点,根据查找法则,我们找到了符合要求的边CI,如下图。并将点I加入到U中。
 继续,此时集合U中有{A,B,C,I}四个点,根绝查找法则,找到符合要求的边CF,如下图。并将点F加入到集合U中。
继续,此时集合U中有{A,B,C,I}四个点,根绝查找法则,找到符合要求的边CF,如下图。并将点F加入到集合U中。
 继续,依照查找法则我们找到边FG,如下图。并将点G加入到U中。
继续,依照查找法则我们找到边FG,如下图。并将点G加入到U中。
 继续,依照查找法则我们找到边GH,如下图。并将点H加入到U中。
继续,依照查找法则我们找到边GH,如下图。并将点H加入到U中。
 继续,依照查找法则我们找到边CD,如下图。并将点D加入到U中。
继续,依照查找法则我们找到边CD,如下图。并将点D加入到U中。
 继续,依照查找法则我们找到边DE,如下图。并将点E加入到U中。
继续,依照查找法则我们找到边DE,如下图。并将点E加入到U中。
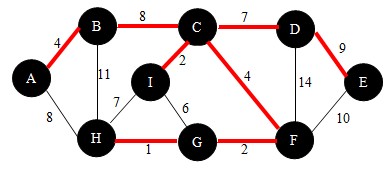 此时,满足U = V,即找到了这颗最小生成树。
此时,满足U = V,即找到了这颗最小生成树。
附注:prim算法最小生成树的生成过程中,也有可能构成回路,需做判断。判断的方法和克鲁斯卡尔算法一样。
http://blog.csdn.net/fengchaokobe/article/details/7521780
好,过程很清楚了,我们来下一下核心算法,算法代码如下:
这就是prim算法的实现。两种算法讲完了。
第三节 结束语
想想,写写,画画......
判断法则:当将边CI加入到已找到边的集合中时,是否会形成回路?
1.如果没有形成回路,那么直接将其连通。此时,对于边的集合又要做一次判断:这两个点是否在已找到点的集合中出现过?
①.如果两个点都没有出现过,那么将这两个点都加入已找到点的集合中;
②.如果其中一个点在集合中出现过,那么将另一个没有出现过的点加入到集合中;
③.如果这两个点都出现过,则不用加入到集合中。
2.如果形成回路,不符合要求,直接进行下一次操作。
根据判断法则,不会形成回路,将点C和点I连通,并将点C和点I加入到集合中。如图:






继续,这次选择边AH,根据判断法则,不会形成回路,将其连通,此时这两个点已经在集合中了,所以不用加入。
继续,这次选择边BC,根据判断法则,会形成回路,直接进行下一次操作。
继续,这次选择边DE,根据判断法则,不会形成回路,将其连通,并将点E加入到集合中。如图:

最后选择边DF,根据法则,会形成回路,不将其连通,也不用加入到集合中。
好了,所有的边都遍历完成了,所有的顶点都在同一个连通分量中,我们得到了这颗最小生成树。
通过生成的过程可以看出,能否得到最小生成树的核心问题就是上面所描述的判断法则。那么,我们如何用算法来描述判断法则呢?我认为只需要三个步骤即可:
⒈将某次操作选择的边XY的两个顶点X和Y和已找到点的集合作比较,如果
①.这两个点都在已找到点的集合中,那么return 2;
②.这两个点有一个在已找到点的集合中,那么return 1;
③这两个点都不在一找到点的集合中,那么return 0;
⒉当返回值为0或1时,可判定不会形成回路;
⒊当返回值为2时,判定能形成回路的依据是:假如能形成回路,设能形成回路的点的集合中有A,B,C,D四个点,那么以点A为起始点,绕环路一周后必能回到点A。如果能回到,则形成回路;如果不能,则不能形成回路。
判定算法很清楚了,我们来写一下克鲁斯卡尔的核心算法,算法代码如下:
- /***图的矩阵存储结构***/
- typedef struct
- {
- VertexType vexs[maxvex]; /***顶点个数***/
- EdgeType arc[maxvex][maxvex]; /***两顶点构成边的权值***/
- }Mgraph;
- /***比较选择的边的两顶点与已找到点的集合***/
- int ComparingPointAndSet(char start, char end, char *StringPoint, int length)
- {
- /***start和end为选择的边的两个顶点
- StringPoint表示已找到点的集合
- length表示StringPoint中现存字符的长度
- ***/
- int index = 0;
- int loop = 0;
- for(; index < length; index++)
- {
- if(start == StringPoint[index])
- {
- loop++;
- continue;
- }
- if(end == StringPoint[index])
- {
- loop++;
- }
- }
- return loop;
- }
- /***判断点是否在集合中出现过***/
- int IsCircleOrNot(char start, char end, int loop, char *StringPoint, int length)
- {
- if(loop == 0) //两个点都没有在集合中出现过
- {
- /***分别加入集合***/
- StringPoint[length] = strat;
- StringPoint[length + 1] = end;
- }
- if(loop == 1) //两点中有一个点在集合中出现过
- {
- /***找出出现过的那个点,并将没有出现过的那个点加入集合***/
- for(int index = 0; index < length; index++)
- {
- if(start == StringPoint[index])
- {
- StringPoint[length] = end;
- break;
- }
- if(end == StringPoint[index])
- {
- StringPoint[length] = start;
- break;
- }
- }
- }
- if(loop == 2) //两个点在集合中都出现过
- {
- JudgeCircle(gph, StringPoint, StringEdge); //是否形成环路
- }
- return 0;
- }
- /***判断是否能形成环路***/
- int JudgeCircle(Mgraph *gph, char *StringPoint, char (*StringEdge)[line], int start, int length)
- {
- /***StringPoint代表已找到顶点的集合
- StringEdge代表已找到边的集合
- start代表判断是否形成回路时的起始点
- length代表StringPoint中现存字符的个数
- ***/
- int index = 0;
- int temp = 0;
- int end = start;
- for(; index < length;index++)
- {
- if(gph->arc[start][index] != 0 && temp != start)
- {
- if(arc[start][index]所代表的边在StringEdge中)
- {
- temp = start; start = index;
- if(index == end)
- {
- //说明形成了环路
- return -1;
- }
- else
- index = 0;
- }
- }
- }
- return 0; //没有形成环路
- }
第二节 普利姆算法(Prim Algorithm)
普利姆算法的核心步骤是:在带权连通图中,从图中某一顶点v开始,此时集合U={v},重复执行下述操作:在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边,将(u,w)这条边加入到已找到边的集合,并且将点w加入到集合U中,当U=V时,就找到了这颗最小生成树。
其实,由步骤我们就可以定义查找法则:在所有u∈U,w∈V-U的边(u,w)∈E中找到一条权值最小的边。
ok,知道了普利姆算法的核心步骤,下面我就用图示法来演示一下工作流程,如图:









附注:prim算法最小生成树的生成过程中,也有可能构成回路,需做判断。判断的方法和克鲁斯卡尔算法一样。
http://blog.csdn.net/fengchaokobe/article/details/7521780
好,过程很清楚了,我们来下一下核心算法,算法代码如下:
- /***图的矩阵存储结构***/
- typedef struct
- {
- VertexType vexs[maxvex]; /***顶点个数***/
- EdgeType arc[maxvex][maxvex]; /***两顶点构成边的权值***/
- }Mgraph;
- int prim(Mgraph *gph, int vexnum)
- /***选择的过程***/
- {
- for(i = 0;i < FoundNum; i++) //FoundNum代表已找到顶点数---FoundPoint[vexnum]
- {
- for(j = 0;j < KnownNum; j++) //KnownNum代表除起始点的其他顶点数---KnownNum[vexnum-1]
- {
- if(gph->arc[i][j] < min && i != j)
- {
- min = gph->arc[i][j];
- }
- }
- if(i == FoundNum - 1)
- {
- MinLength += gph->arc[i][j]; MinLength代表最小权值和
- gph->arc[i][j] = INFITY; //找到这条最小边后,将其权值置为maxmun,以后遇到这条边时直接跳过
- FoundPoint[FoundNum] = j; //将顶点j加入到已找到顶点数的集合中
- FoundNum++;
- i= 0; //进行下一次操作
- min = INFITY;
- }
- //找到这条边之后判断是否会形成环路,判断函数见克鲁斯卡尔的环路判断函数JudgeCircle()
- }
- return 0;
- }
第三节 结束语
想想,写写,画画......