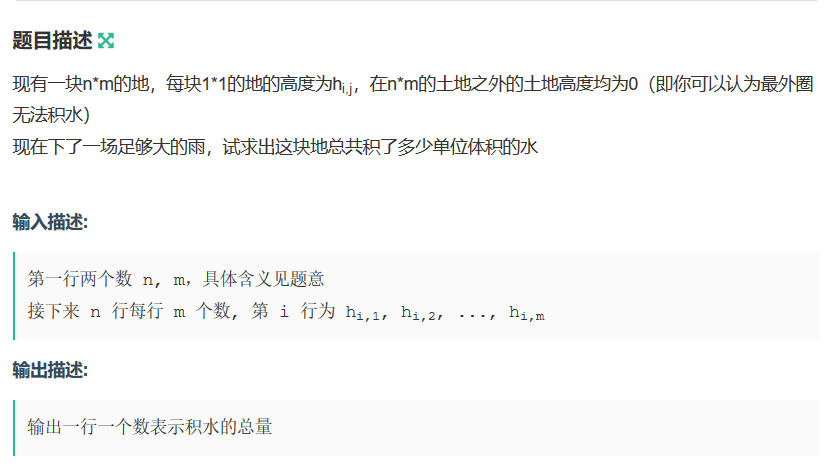
问题一
Input:
5 5
0 0 5 0 0
0 4 3 8 2
9 5 7 2 7
1 9 6 5 4
1 0 0 6 2
Output:
4
Input:
10 10
0 0 0 0 0 0 0 0 0 0
0 5 2 6 4 3 1 7 8 0
0 6 4 2 3 5 1 4 6 0
0 3 6 4 1 2 4 7 8 0
0 2 5 5 1 2 3 4 4 0
0 2 3 1 5 4 4 1 4 0
0 4 1 2 3 4 5 2 1 0
0 7 5 5 1 5 4 5 7 0
0 1 3 5 5 4 6 8 7 0
0 0 0 0 0 0 0 0 0 0
Output:
23
Hint:
- 对于10%的数据, n, m ≤ 4, h ≤ 5;
- 对于前50%的数据, n, m ≤ 20, h ≤ 10;
- 对于前70%的数据, n, m ≤ 100, h ≤ 50;
- 对于另外10%的数据, 不存在两个连续的块能积水;
- 对于95%的数据, n, m ≤ 500, h ≤ 100.
- 对于100%的数据, n, m ≤ 1000, h ≤ 1000,000,000.
1 #include<iostream> 2 #include<cstdio> 3 #include<queue> 4 #include<cstring> 5 using namespace std; 6 7 const int N = 1e3+3; 8 9 int xy[4][2]={-1, 0, 0, -1, 0, 1, 1, 0}; 10 11 struct pnt{ 12 int x,y,h; 13 bool operator<(const pnt a)const{ 14 return h>a.h; 15 } 16 }; 17 18 priority_queue<pnt>q; 19 20 int h[N][N],f[N][N]; 21 22 int main() 23 { 24 int n,m,i,j; 25 cin >> n >> m; 26 memset(f,-1,sizeof(f)); 27 for (i = 1; i <= n; i++) 28 for (j = 1; j <= m; j++){ 29 cin >> h[i][j]; 30 if (i == 1 || j == 1 || i == n || j == m) 31 q.push((pnt){i, j, h[i][j]}), f[i][j] = 0; 32 } 33 while (!q.empty()){ 34 pnt v = q.top(); 35 q.pop(); 36 for (i = 0; i < 4; i++) { 37 int dx = v.x+xy[i][0], dy = v.y + xy[i][1]; 38 if (dx > 0 && dx <= n && dy > 0 && dy <= m && f[dx][dy] == -1){ 39 q.push((pnt){dx, dy, h[dx][dy]}); 40 f[dx][dy] = max(f[v.x][v.y], v.h); 41 } 42 } 43 } 44 long long ans = 0; 45 for (i = 1; i <= n; i++) 46 for (j = 1;j <= m; j++) 47 ans += max(f[i][j]-h[i][j], 0); 48 cout << ans << endl; 49 }
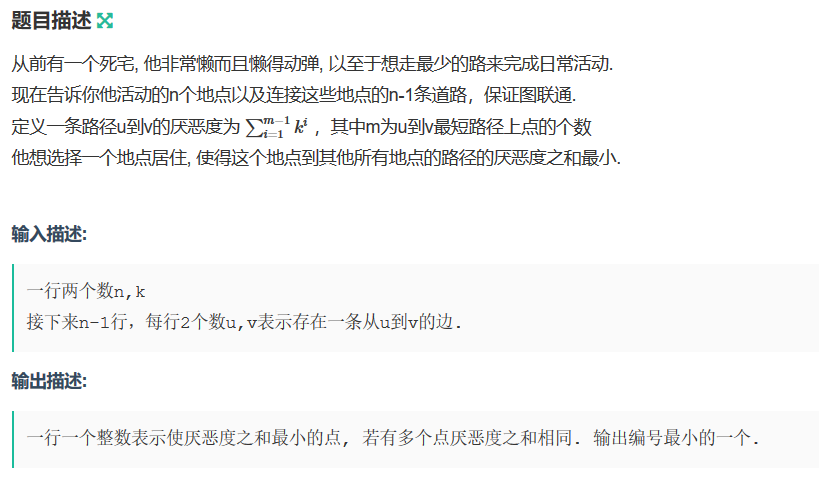
问题二:
Input:
4 2
1 2
2 3
2 4
Output:
2
Hint:
2号点到1, 3, 4点的路径的厌恶度都是2,厌恶度总和为 6
1, 3, 4到其它点的路径厌恶度之和均为2 + 6 + 6 = 14
数据范围
- 对于前10%的数据, n ≤ 10;
- 对于另外20%的数据, n ≤ 500 且 保证图为一条链;
- 对于另外20%的数据, n ≤ 500, k = 2;
- 对于另外20%的数据, k = 1;
- 对于100%的数据,n ≤ 20000, k ≤ 10,除 对于20%的数据保证图为一条链外 图保证随机!!!
#include<bits/stdc++.h>
using namespace std;
#define Uni All Right
#define REP(i,a,b) for(int i=(a),i##_end_=(b);i<i##_end_;++i)
#define DREP(i,a,b) for(int i=(a),i##_end_=(b);i>i##_end_;--i)
#define LCREP(i,a) for(int &i=Cur[a];i;i=Next[i])
#define LREP(i,a) for(int i=Head[a];i;i=Next[i])
#define LL long long
#define DB double
static const int M=22;
int n,m,T,v;
DB Tmp;
struct Node{
DB V[M][M];
void Clear(){memset(V,0,sizeof(V));}
void Init(DB p){
Clear();
REP(i,0,m){
if(i==m-1)p=0;
V[i][i]=1-p;
V[i][i+1]=p;
V[i][m]=i;
}
V[m][m]=1;
}
Node operator *(const Node &_)const{
Node P;P.Clear();
REP(i,0,m+1)REP(j,0,m+1)REP(k,0,m+1)
P.V[i][j]+=V[i][k]*_.V[k][j];
return P;
}
}K,Ans;
int main(){
scanf("%d%d%d%d",&n,&m,&T,&v);
m-=n,Tmp+=1.0*n*T+(T-1);
Ans.V[0][0]=1;
for(int l=1,r;l<T;l=r){
r=T/(T/(l+1));
K.Init(T/r*1.0/T);
int p=r-l;
for(;p;K=K*K,p>>=1)if(p&1)Ans=Ans*K;
}
printf("%.9lf
",(Ans.V[0][m]+Tmp)*v);
return 0;
}
问题三:

Input:
6 10 1 1
Output:
6
Hint:
第0个时刻它有100%的概率新建一个SCV.
此时6个SCV采了6单位晶体.
第1时刻采集矿物完成,共采集6单位晶体.
- 对于30%的数据, 满足 T <= 106;
- 对于另外10%的数据满足 m = n+1;
#include<bits/stdc++.h>
using namespace std;
#define Uni All Right
#define REP(i,a,b) for(int i=(a),i##_end_=(b);i<i##_end_;++i)
#define DREP(i,a,b) for(int i=(a),i##_end_=(b);i>i##_end_;--i)
#define LCREP(i,a) for(int &i=Cur[a];i;i=Next[i])
#define LREP(i,a) for(int i=Head[a];i;i=Next[i])
#define LL long long
#define DB double
static const int M=22;
int n,m,T,v;
DB Tmp;
struct Node{
DB V[M][M];
void Clear(){memset(V,0,sizeof(V));}
void Init(DB p){
Clear();
REP(i,0,m){
if(i==m-1)p=0;
V[i][i]=1-p;
V[i][i+1]=p;
V[i][m]=i;
}
V[m][m]=1;
}
Node operator *(const Node &_)const{
Node P;P.Clear();
REP(i,0,m+1)REP(j,0,m+1)REP(k,0,m+1)
P.V[i][j]+=V[i][k]*_.V[k][j];
return P;
}
}K,Ans;
int main(){
scanf("%d%d%d%d",&n,&m,&T,&v);
m-=n,Tmp+=1.0*n*T+(T-1);
Ans.V[0][0]=1;
for(int l=1,r;l<T;l=r){
r=T/(T/(l+1));
K.Init(T/r*1.0/T);
int p=r-l;
for(;p;K=K*K,p>>=1)if(p&1)Ans=Ans*K;
}
printf("%.9lf
",(Ans.V[0][m]+Tmp)*v);
return 0;
}