小V和gcd树（树链剖分）

小V和gcd树

一场只会一签到题的比赛，还记得当时我写这道题，直接暴力，给我TLE的啊，，，，

过了也有一段时间了，我带着树链剖分回来再写这道题，终于给它A了。

思路

这道题目不完全像树链？？？树链不是维护点的权值吗，怎么这题要维护边的权值。

确实这道题是通过点来改变边的权值的，我们考虑如何通过点去得到其走过的边，下面我先通过图片模拟题目给的样例。

图片是基于点(1)为根节点的剖分图，红色的圈圈的是重链。

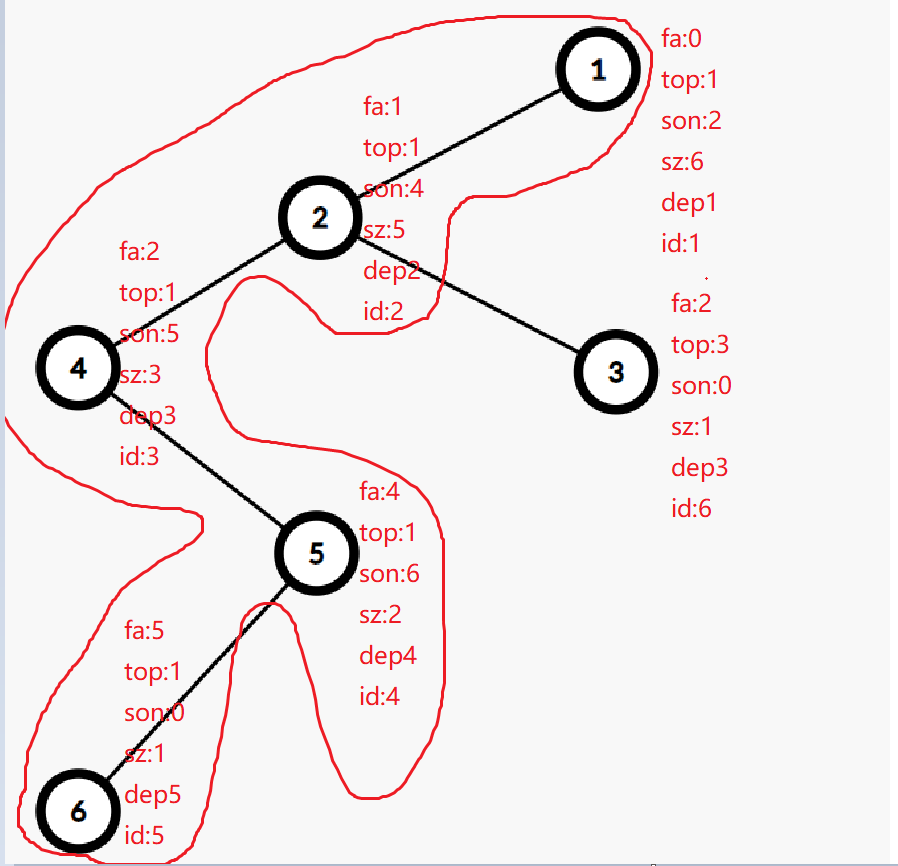
rk	point
1	1
2	2
3	4
4	5
5	6
6	3

我们先约定处理边权的方式，如果当前节点不是顶节点，我们记录(dis[id[now]] = gcd(value[now], value[fa[now]]))

也就是当前节点的dfs序编号为index的dis数组中存的是当前节点与其父节点的边权值。

假设我们要求的是3 —> 4的边权值。

开始这两个点不在同一条重链上，因此我们应该首先移动点3，当碰到top节点的时候要特殊考虑，因为这个点与其父节点的dis没有记录，所以我们每次碰到top节点的时候特殊求一下，在这里也就是求(gcd(value[2], valu[3]))，然后3走到节点2了，此时这两个节点在同一条重链上，我们只需要进行如下操作。

for(int i = id[2] + 1; i <= id[4]; i++)
    ans += dis[i];

舍弃最上面的节点，因为最上面的节点记录的边在这一段中没有用，然后去求其余边的权值。

---

那么我们因该如何更新点呢。

有了上面的处理方式，一个节点的边权最多只会影响两条边，一条是与其父节点相连的边，另一条是与其重儿子相连的边。所以我们只需要更新这两条边就行了，当然每次我们更新的时候也要考虑这个节点是不是top节点的情况。

代码

#include <bits/stdc++.h>

using namespace std;

const int N = 2e4 + 10;


int head[N], value[N], to[N << 1], nex[N << 1], cnt;
int fa[N], top[N], son[N], sz[N], dep[N], rk[N], id[N], tot;
int ans[N], n, m;

int gcd(int a, int b) {
    return b ? gcd(b, a % b) : a;
}

void add(int x, int y) {
    to[cnt] = y;
    nex[cnt] = head[x];
    head[x] = cnt++;
}

void dfs1(int rt, int f) {
    // cout << rt << " " << f << endl;
    dep[rt] = dep[f] + 1;
    fa[rt] = f, sz[rt] = 1;
    for(int i = head[rt]; ~i; i = nex[i]) {
        if(to[i] == f)  continue;
        dfs1(to[i], rt);
        sz[rt] += sz[to[i]];
        if(!son[rt] || sz[to[i]] > sz[son[rt]])
            son[rt] = to[i];
    }
}

void dfs2(int rt, int t) {
    top[rt] = t;
    id[rt] = ++tot;
    rk[tot] = rt;
    if(rt != t)   ans[id[rt]] = gcd(value[rt], value[fa[rt]]);
    if(!son[rt])    return ;
    dfs2(son[rt], t);
    for(int i = head[rt]; ~i; i = nex[i]) {
        if(to[i] == fa[rt] || to[i] == son[rt]) continue;
        dfs2(to[i], to[i]);
    }
}

int query(int x, int y, int w) {
    int sum = 0;
    while(top[x] != top[y]) {
        if(dep[top[x]] < dep[top[y]])   swap(x, y);
        for(int i = id[top[x]] + 1; i <= id[x]; i++)
            if(ans[i] <= w) sum++;
        if(gcd(value[top[x]], value[fa[top[x]]]) <= w)  sum++;
        x = fa[top[x]];
    }
    if(dep[x] > dep[y]) swap(x, y);
    for(int i = id[x] + 1; i <= id[y]; i++)
        if(ans[i] <= w) sum++;
    return sum;
}


int main() {
    // freopen("in.txt", "r", stdin);
    scanf("%d %d", &n, &m);
    for(int i = 1; i <= n; i++)
        scanf("%d", &value[i]);
    int x, y, w, op;
    memset(head, -1, sizeof head), cnt = 0;
    for(int i = 1; i < n; i++) {
        scanf("%d %d", &x, &y);
        add(x, y);
        add(y, x);
    }
    dfs1(1, 0);
    dfs2(1, 1);
    // for(int i = 1; i <= n; i++)
    //     printf("%d
fa:%d
top:%d
son:%d
sz:%d
dep%d
id:%d

", i, fa[i], top[i], son[i], sz[i], dep[i], id[i]);
    for(int i = 1; i <= m; i++) {
        scanf("%d", &op);
        if(op == 1) {
            scanf("%d %d", &x, &w);
            value[x] = w;
            if(top[x] != x)     ans[id[x]] = gcd(value[x], value[fa[x]]);
            if(son[x])          ans[id[son[x]]] = gcd(value[x], value[son[x]]);
        }
        else {
            scanf("%d %d %d", &x, &y, &w);
            printf("%d
", query(x, y, w));
        }
    }
    return 0;
}