K Best
Time Limit: 8000MS Memory Limit: 65536K
Total Submissions: 17073 Accepted: 4286
Case Time Limit: 2000MS Special Judge
Description
Demy has n jewels. Each of her jewels has some value vi and weight wi.
Since her husband John got broke after recent financial crises, Demy has decided to sell some jewels. She has decided that she would keep k best jewels for herself. She decided to keep such jewels that their specific value is as large as possible. That is, denote the specific value of some set of jewels S = {i1, i2, …, ik} as
.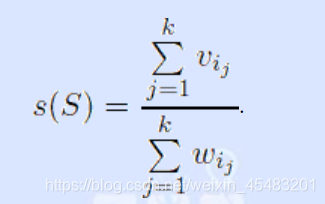
Demy would like to select such k jewels that their specific value is maximal possible. Help her to do so.
Input
The first line of the input file contains n — the number of jewels Demy got, and k — the number of jewels she would like to keep (1 ≤ k ≤ n ≤ 100 000).
The following n lines contain two integer numbers each — vi and wi (0 ≤ vi ≤ 106, 1 ≤ wi ≤ 106, both the sum of all vi and the sum of all wi do not exceed 107).
Output
Output k numbers — the numbers of jewels Demy must keep. If there are several solutions, output any one.
Sample Input
3 2
1 1
1 2
1 3
Sample Output
1 2
还是这题,其实有点像是解方程里的找零点,二分的思想也是一样,但是这篇讲的是一个更加高效的算法,牛顿迭代法。

这是百度给出的解读:
对于普通的二次或者更加高次的函数找零点我们可以,先找一个近似点x。于是我们有直线 y = f(x。)’(x - x。)
通过迭代x = x。- f(x。) / f(x。)’
再不断的通过x去找下面的更加精确的x,通过比对这两次的差值,把答案控制在一个课允许的范围内就行。
在这道题目中,迭代公式就变成了,sigma(vi) / sigma(wi) = s,然后通过s去优化v - w * s ,最后得到在精度允许的范围内的s
#include <iostream>
#include <cmath>
#include <algorithm>
#include <cstdio>
using namespace std;
const int maxn = 100010;
int n, m;
struct each {
double sum, v, w;
int id;
}select[maxn];
bool cmp(each a, each b) {
return a.sum > b.sum;
}
double judge() {//迭代,
double sum1 = 0, sum2 = 0;
for(int i = 1; i <= m; i++)
sum1 += select[i].v, sum2 += select[i].w;
return sum1 / sum2;
}
int main() {
while(scanf("%d %d", &n, &m) != EOF) {
for(int i = 1; i <= n; i++) {
scanf("%lf %lf", &select[i].v, &select[i].w);
select[i].id = i;
}
double s1= 0, s2 = judge();
while(abs(s2 - s1) >= 1e-7) {
s1 = s2;
for(int i = 1; i <= n; i++)
select[i].sum = select[i].v - select[i].w * s2;
sort(select + 1, select + n + 1,cmp);
s2 = judge();
}
cout << select[1].id ;
for(int i = 2; i <= m; i++)
cout << " " << select[i].id ;
cout << endl;
}
return 0;
}