jQuery火箭图标返回顶部代码

      MSCN系数是无参考的空间域图像质量评估算法BRISQUE（No-Reference Image Quality Assessment in the Spatial Domain）中提出的，MSCN系数具有由于失真的存在而改变的特征统计特性，并且量化这些变化将使得可以预测影响图像的失真类型以及其感知质量。这篇论文的大致原理是从图像中提取MSCN系数，然后将MSCN系数拟合成非对称性广义高斯分布，提取拟合的高斯分布的特征，输入到支持向量机SVM中做回归，最终得到图像质量的评分。

       这篇论文提供了源代码，其中有MSCN的计算代码，但是论文中的关于证明不同失真图像的MSCN系数具有不同分布的直方图的代码并没有，经过大概大半天的时间，我把这个直方图用matlab做了出来。

      首先，直观的看一下MSCN系数图如下（原图和MSCN系数图）：

       

                                                                                                                                                

MSCN系数图的计算公式源论文中有，代码从源代码中修改而来，如下：

clear;clc;
imdist=imread('2.png');

%imshow(imdist); %显示原图
imdist = rgb2gray(imdist);
imdist = double(imdist);

%imdist=phasecong3(imdist);
%imshow(phaseCong)

window = fspecial('gaussian',7,7/6);
window = window/sum(sum(window));

mu            = filter2(window, imdist, 'same');
mu_sq         = mu.*mu;
sigma         = sqrt(abs(filter2(window, imdist.*imdist, 'same') - mu_sq));
structdis     = (imdist-mu)./(sigma+1);


%imshow(structdis,[]);  %显示MSCN图

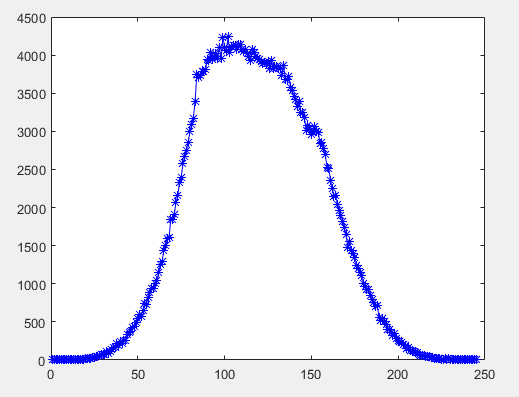
　　其实MSCN系数计算出来是一个浮点数矩阵，就是上面代码中的structdis，范围是-2到2。论文中的SMCN系数直方图横坐标表示图像的MSCN系数值，纵坐标表示值出现的频率，在网上找了好久，发现并没有源代码，只好自己写了。刚开始的时候以为每个值会出现多次，统计了一下发现绝大多数MSCN值仅出现了一次，后来才想明白，横坐标表示的不是每一个MSCN值的频率，而是一个范围值的频率。浮点数不好统计，于是刚开始的时候我把MSCN系数的值转化到了0-255，然后再来统计它的频率，统计个数用的是matlab自带的函数tabulate，做出的图如下：

具体代码如下：

clear;clc;
imdist=imread('2.png');

%imshow(imdist);
imdist = rgb2gray(imdist);
imdist = double(imdist);

%imdist=phasecong3(imdist);
%imshow(phaseCong)

window = fspecial('gaussian',7,7/6);
window = window/sum(sum(window));

mu            = filter2(window, imdist, 'same');
mu_sq         = mu.*mu;
sigma         = sqrt(abs(filter2(window, imdist.*imdist, 'same') - mu_sq));
structdis     = (imdist-mu)./(sigma+1);


%imshow(structdis,[]);  %显示MSCN图
% imshow(mu,[]);
% imshow(sigma,[]);
%hist(structdis);

  InImg=structdis;
  ymax=255;ymin=0;
  xmax = max(max(InImg)); %求得InImg中的最大值
  xmin = min(min(InImg)); %求得InImg中的最小值
  OutImg = round((ymax-ymin)*(InImg-xmin)/(xmax-xmin) + ymin); %归一化并取整

%hist(structdis);

n=tabulate(OutImg(:)); %计算矩阵中各元素出现的频数
number=n(:,2);

a=number;

x=1:1:245;
plot(x,a,'-*b'); %绘图

　　其他问题先不说，首先就是点太密集了，跟论文中的完全不一样，而且MSCN值转化到0-255之后可能会丢失一些精度。所以这个不合格。然后原因出在matlab自带的统计矩阵值个数的函数上，这个函数不靠谱，只能自己写了，倒不是很麻烦，循环统计范围值就好了，但是以前写c++习惯了，用matlab写的时候总是想着c++的方式来写，结果很简单的问题头都搞晕了，还好有好朋友帮忙，循环很快写出来了。然后封装成函数如下（以下的图来自TID2013的bike.bmp）：

function [n]=compute_mscn(imdist)    %计算图像的MSCN系数并统计其像素值出现的频数

%imdist=imread('3.png');
imdist = rgb2gray(imdist);
imdist = double(imdist);

%imdist=phasecong3(imdist);
%imshow(phaseCong)

window = fspecial('gaussian',7,7/6);
window = window/sum(sum(window));

mu            = filter2(window, imdist, 'same');
mu_sq         = mu.*mu;
sigma         = sqrt(abs(filter2(window, imdist.*imdist, 'same') - mu_sq));
structdis     = (imdist-mu)./(sigma+1);
% imshow(structdis,[]);  %显示MSCN图
% imshow(mu,[]);
% imshow(sigma,[]);
%hist(structdis);

  InImg=structdis;
  ymax=255;ymin=0;
  xmax = max(max(InImg)); %求得InImg中的最大值
  xmin = min(min(InImg)); %求得InImg中的最小值
  OutImg = round((ymax-ymin)*(InImg-xmin)/(xmax-xmin) + ymin); %归一化并取整

%hist(structdis);

%n=tabulate(OutImg(:)); %计算矩阵中各元素出现的频数
%number=n(:,2);

%a=number;
for j=1:52         %统计MSCN系数出现的频数
    i=(j-1)*5;
    n(j)=length(find(OutImg>=i&OutImg<i+2));
    % t=t+1;
end
end

　　调用的代码也很简单，如下所示：

imdist=imread('bikes.bmp');
n1=compute_mscn(imdist);

imdist=imread('img15.bmp');
n2=compute_mscn(imdist);

imdist=imread('img31.bmp');
n3=compute_mscn(imdist);

imdist=imread('img129.bmp');
n4=compute_mscn(imdist);

x=0:5:255;
%x=-2:0.05:2;
plot(x,n1,'-*b',x,n2,'-dr',x,n3,'-sg',x,n4,'-ok');
set(gca,'XTick',[0:50:250])
%set(gca,'XTick',[-2:0.5:2]);%x轴范围，间隔0.5
legend('org','jp2k','ff','gblur');   %右上角标注
xlabel('MSCN系数')  %x轴坐标描述
ylabel('频数（归一化）') %y轴坐标描述
grid on;  %加网格线
%set(gca,'GridLineStyle',':','GridColor','k','GridAlpha',1); %加网格虚线

　　然后结果图如下：

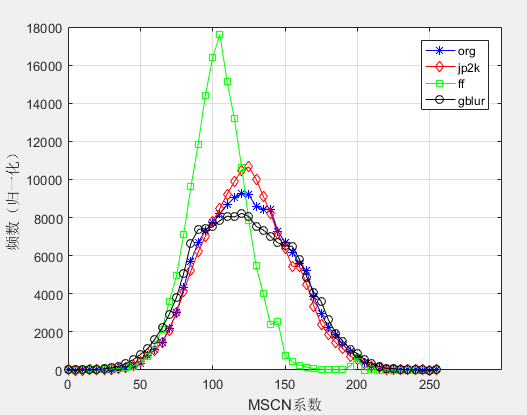
理论上和论文中的意思是一样了，但是还是有些差距，首先是MSCN系数的值被归一化到0-255了，然后频数还没有归一化，所以考虑不把MSCN系数的值转换到0-255，直接进行统计，以免有误差，代码仍然进行了封装，函数如下：

function [n]=compute_mscn2(imdist)    %计算图像的MSCN系数并统计其像素值出现的频数

imdist = rgb2gray(imdist);
imdist = double(imdist);

%imdist=phasecong3(imdist);
%imshow(phaseCong)

window = fspecial('gaussian',7,7/6);
window = window/sum(sum(window));

mu            = filter2(window, imdist, 'same');
mu_sq         = mu.*mu;
sigma         = sqrt(abs(filter2(window, imdist.*imdist, 'same') - mu_sq));
structdis     = (imdist-mu)./(sigma+1);
% imshow(structdis,[]);  %显示MSCN图
% imshow(mu,[]);
% imshow(sigma,[]);
%hist(structdis);

for j=1:81              %统计MSCN系数出现的频数
    i=(j-40)*0.05;
    n(j)=length(find(structdis >=i&structdis<i+0.05));
    % t=t+1;
end
n=mapminmax(n,0,1);

end

　　调用的代码如下：

imdist=imread('bikes.bmp');
n1=compute_mscn2(imdist);

imdist=imread('img15.bmp');
n2=compute_mscn2(imdist);

imdist=imread('img31.bmp');
n3=compute_mscn2(imdist);

imdist=imread('img129.bmp');
n4=compute_mscn2(imdist);

%x=0:5:255;
x=-2:0.05:2;
plot(x,n1,'-*b',x,n2,'-dr',x,n3,'-sg',x,n4,'-ok');
%set(gca,'XTick',[0:50:250])
set(gca,'XTick',[-2:0.5:2]);%x轴范围，间隔0.5
legend('org','jp2k','ff','gblur');   %右上角标注
xlabel('MSCN系数')  %x轴坐标描述
ylabel('频数（归一化）') %y轴坐标描述
grid on;  %加网格线
%set(gca,'GridLineStyle',':','GridColor','k','GridAlpha',1); %加网格虚线

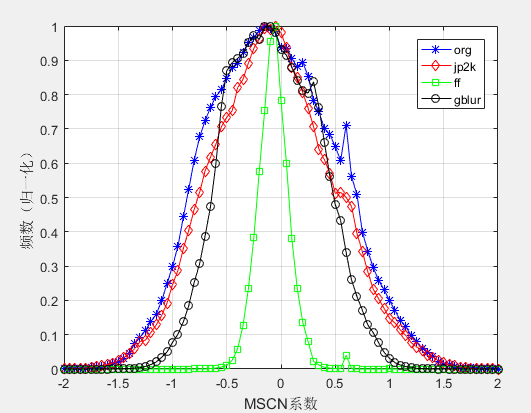
　　最终总算是完成任务了，可以看出确实不同失真图像的MSCN系数具有不同的直方图分布，图如下：