KNN算法
基本模型:给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例。这k个实例的多数属于某个类,就把输入实例分为这个类。
KNN没有显式的学习过程。
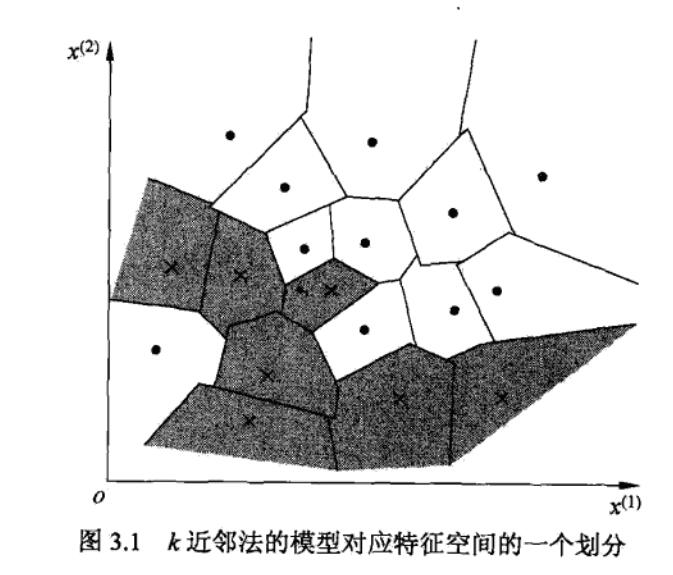
KNN使用的模型实际上对应于特征空间的划分。特征空间中,对每个训练实例点(x_i),距离该点比其它点更近的所有点组成一个区域,叫作单元(cell)。每个训练实例拥有一个单元。所有的训练实例点的单元构成对特征空间的一个划分。如下图所示。
三要素:KNN模型由三个基本要素——距离度量,K值选择,分类决策决定。当三要素和训练集确定后,对任何一个新的输入实例,它所属的类唯一地确定。
KNN三要素之1——距离度量
由不同的距离度量所确定的最近邻点是不同的。
KNN的特征空间一般是n维实数向量空间(R^n),使用的距离是欧氏距离。但也可以是其他距离,如更一般的(L_p)距离。设(x_i)为第(i)个样本,(n)维向量,(x_i = (x_i^{(1)}, x_i^{(2)}, ..., x_i^{(n)})^T),则
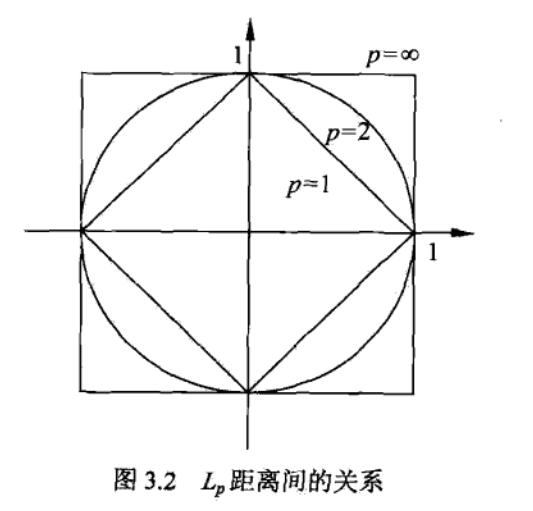
(p=2)时称为欧式距离,(p=1)称为曼哈顿距离。下图是二维空间中,与原点的(L_p)距离为1的图形。
(p=1)时,(|x| + |y| = 1)
(p=2)时,(x^2 + y^2 = 1)
(p=infty)时,(max(|x|, |y|) = 1)
KNN三要素之2——K值选择
K值的选择会对KNN结果产生重大影响
选择较小的K值:
如果选择较小的K值,相当于用较小的邻域中的训练实例进行预测,只有与输入实例较近的训练实例才会对预测结果起作用。“学习”的近似误差会减小。
缺点是“学习”的估计误差会增大,预测结果对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。
K值的减小意味着整体模型变得复杂,容易发生过拟合。
选择较大的K值:
如果选择较大的K值,相当于用较大邻域中的训练实例进行预测。其优点是减小学习的估计误差,缺点是近似误差会增大。这时离输入实例较远的训练实例起预测作用,使预测发生错误。
K值的增大意味着整体模型变得简单。K=N时,无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类,这时模型过于简单,完全忽略训练实例中的大量有用信息,是不可取的。
在应用中:
K值一般取一个比较小的数值,通常采用交叉验证法来选取最优的K值。
KNN三要素之3——分类决策规则
KNN的分类决策规则往往是多数表决,即由输入实例的K个邻近的训练实例中的多数类决定输入实例的类。
KNN的实现:kd树
kd树:KNN最简单的实现方法是线性扫描。这时要计算输入实例与每一个训练实例的距离。当训练集很大时,计算非常耗时,这种方法是不可行的。
为了提高KNN搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数。具体方法很多,下面介绍其中的kd树方法。
构造kd树:kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是二叉树,表示对k维空间的一个划分。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分,构成一系列的k维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。
通常,依次选择坐标轴对空间切分,选择训练实例点在选定坐标轴上的中位数为切分点,这样得到的kd树是平衡的。注意,平衡的kd树搜索时的效率未必是最优的。
算法3.2 (构造平衡kd树)
输入:k维空间数据集(T = {x_1, x_2, ..., x_N}),其中(x_i = (x_i^{(1)}, x_i^{(2)}, ..., x_i^{(k)})^T),(i = 1, 2, ..., N);
输出:kd树
(1)开始:构造根结点,根结点对应于包含(T)的k维空间的超矩阵区域。
选择(x^{(1)})为坐标轴,以(T)中所有实例的(x^{(1)})坐标的中位数为切分点,将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴(x^{(1)})垂直的超平面实现。
由根结点生成的深度为1的左右子结点:左结点对应坐标(x^{(1)})小于切分点的子区域,右结点对应坐标(x^{(1)})大于切分点的子区域。将落在切分超平面上的实例点保存在根结点。
(2)重复:对深度为(j)的结点,选择(x^{(j)})为切分的坐标轴,(l = j(mod k) + 1),以该结点的区域中所有实例的(x^{(l)})坐标的中位数为切分点。
由该结点生成深度为(j+1)的左右子结点:左结点对应坐标(x^{(l)})小于切分点的子区域,右结点对应坐标(x^{(l)})大于切分点的子区域。将落在切分超平面上的实例点保存在该结点。
(3)直到两个子区域没有实例存在时停止,从而形成kd树的区域划分。
搜索kd树:利用kd树可以省去对大部分数据点的搜索,从而减少搜索的计算量。这里以最近邻为例加以叙述。
算法3.3 (用kd树的最近邻搜索)
输入:已构造的kd树;目标点x;
输出:x的最近邻
(1)从根结点出发,递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标,则左移,否则右移,直到子结点为叶结点。
(2)以此叶结点为“当前最近点”。
(3)递归向上回退,在每个结点进行以下操作:
(a)若该结点保存的实例点比“当前最近点”离目标点更近,则以该实例点为“当前最近点”。
(b)检查另一子结点对应的区域是否与“以目标点为球心,以目标前与‘当前最近点’的距离为半径的超球体”相交。
如果相交,可能在另一子结点对应的区域内存在距离目标点更近的点,移动到另一结点,递归搜索。
如果不相交,向上回退。
(4)回退到根结点时,搜索结束。最后的“当前最近点”即为x的最近邻点。
