在数据分析和数据挖掘的过程中,我们经常需要知道个体间差异的大小,进而评价个体的相似性和类别。最常见的是数据分析中的相关分析,数据挖掘中的分类和聚类算法,如K最近邻(KNN)和K均值(K-Means)。当然衡量个体差异的方法有很多,这里整理罗列下。
为了方便下面的解释和举例,先设定我们要比较X个体和Y个体间的差异,它们都包含了N个维的特征,即X=(x1, x2, x3, … xn),Y=(y1, y2, y3, … yn)。下面来看看主要可以用哪些方法来衡量两者的差异,主要分为距离度量和相似度度量。
距离度量
距离度量(Distance)用于衡量个体在空间上存在的距离,距离越远说明个体间的差异越大。
曼哈顿距离(Manhattan Distance)
曼哈顿距离来源于城市街区距离,是将多个维度上的距离进行求和后的结果,如下:
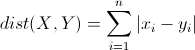
欧几里得距离(Euclidean Distance)
欧氏距离是最常见的距离度量,衡量的是多维空间中各个点之间的绝对距离。公式如下:
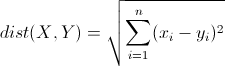
切比雪夫距离(Chebyshev Distance)
切比雪夫距离起源于国际象棋中国王的走法,我们知道国际象棋国王每次只能往周围的8格中走一步,那么如果要从棋盘中A格(x1, y1)走到B格(x2, y2)最少需要走几步?你会发现最少步数总是max( | x2-x1 | , | y2-y1 | ) 步 。扩展到多维空间,其实切比雪夫距离就是当p趋向于无穷大时的明氏距离:
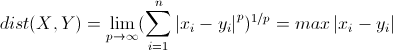
明可夫斯基距离(Minkowski Distance)
简称明氏距离,是欧氏距离的推广,是对多个距离度量公式的概括性的表述。公式如下:
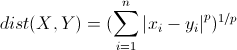
上面的曼哈顿距离、欧氏距离和切比雪夫距离都是明氏距离在特殊条件下的应用,这些距离都存在明显的缺点。
举个例子:二维样本(身高,体重),其中身高范围是150~190,体重范围是50~60,有三个样本:a(180,50),b(190,50),c(180,60)。那么a与b之间的明氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c之间的明氏距离,但是身高的10cm真的等价于体重的10kg么?因此用明氏距离来衡量这些样本间的相似度很有问题。
简单说来,缺点主要有两个:(1)将各个分量的量纲(scale),也就是“单位”当作相同的看待了。(2)没有考虑各个分量的分布(期望,方差等)可能是不同的。可通过对各分量标准化来修正,即使各分量都服从高斯分布。
马哈拉诺比斯距离(Mahalanobis Distance)
简称马氏距离。

若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式就成了:

也就是欧氏距离了。若协方差矩阵是对角矩阵,公式变成了标准化欧氏距离。马氏距离的优缺点:量纲无关,排除变量之间的相关性的干扰。
汉明距离(Hamming distance)
两个等长字符串s1与s2之间的汉明距离定义为将其中一个变为另外一个所需要作的最小替换次数。例如字符串“1111”与“1001”之间的汉明距离为2。
应用:信息编码(为了增强容错性,应使得编码间的最小汉明距离尽可能大)
相似度度量
相似度度量(Similarity),即计算个体间的相似程度,与距离度量相反,相似度度量的值越小,说明个体间相似度越小,差异越大。
简单匹配相似系数(Simple Matching Coefficient)
Common situation is that objects, p and q, have only binary attributes
M01 = the number of attributes where p was 0 and q was 1
M10 = the number of attributes where p was 1 and q was 0
M00 = the number of attributes where p was 0 and q was 0
M11 = the number of attributes where p was 1 and q was 1
SMC = number of matches / number of attributes = (M11 + M00) / (M01 + M10 + M11 + M00)
缺点:对于p,q比较稀疏,或者说p,q中0值比较多时,结果会相似度比较高,可用Jaccard相似系数解决
Jaccard相似系数(Jaccard Coefficient)
上面的Jaccard系数 J = number of 11 matches / number of not-both-zero attributes values = (M11) / (M01 + M10 + M11)
Jaccard系数主要用于计算符号度量或布尔值度量的个体间的相似度,因为个体的特征属性都是由符号度量或者布尔值标识,因此无法衡量差异具体值的大小,只能获得“是否相同”这个结果,所以Jaccard系数只关心个体间共同具有的特征是否一致这个问题。如果比较X与Y的Jaccard相似系数,只比较xn和yn中相同的个数,公式如下:
![]()
余弦相似度(Cosine Similarity)
余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比距离度量,余弦相似度更加注重两个向量在方向上的差异,而非距离或长度上。公式如下:
![]()
调整余弦相似度(Adjusted Cosine Similarity)
虽然余弦相似度对个体间存在的偏见可以进行一定的修正,但是因为只能分辨个体在维之间的差异,没法衡量每个维数值的差异,会导致这样一个情况:比如用户对内容评分,5分制,X和Y两个用户对两个内容的评分分别为(1,2)和(4,5),使用余弦相似度得出的结果是0.98,两者极为相似,但从评分上看X似乎不喜欢这2个内容,而Y比较喜欢,余弦相似度对数值的不敏感导致了结果的误差,需要修正这种不合理性,就出现了调整余弦相似度,即所有维度上的数值都减去一个均值,比如X和Y的评分均值都是3,那么调整后为(-2,-1)和(1,2),再用余弦相似度计算,得到-0.8,相似度为负值并且差异不小,但显然更加符合现实。
皮尔森相关系数(Pearson Correlation Coefficient)
就是我们平常所说的相关系数,公式如下: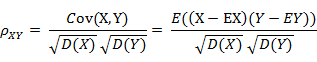
相关系数是衡量随机变量X与Y相关程度的一种方法,相关系数的取值范围是[-1,1]。相关系数的绝对值越大,则表明X与Y相关度越高。当X与Y线性相关时,相关系数取值为1(正线性相关)或-1(负线性相关)。
在Mahout中,皮尔森相关系数的计算是针对两个向量中重叠的部分(The similarity computation can only operate on items that both users have expressed a preference for),有以下几个缺点:First, it doesn’t take into account the number of items in which two users’ preferences overlap; Second, if two users overlap on only one item, no correlation can be computed because of how the computation is defined. Finally, the correlation is also undefined if either series of preference values are all identical.
The cosine measure similarity and Pearson correlation aren’t the same thing, but if you bother to work out the math, you’ll discover that they actually reduce to the same computation when the two series of input values each have a mean of 0 (centered). The Mahout implementation centers the input, so the two are the same.
欧氏距离与余弦相似度
欧氏距离是最常见的距离度量,而余弦相似度则是最常见的相似度度量,很多的距离度量和相似度度量都是基于这两者的变形和衍生,所以下面重点比较下两者在衡量个体差异时实现方式和应用环境上的区别。
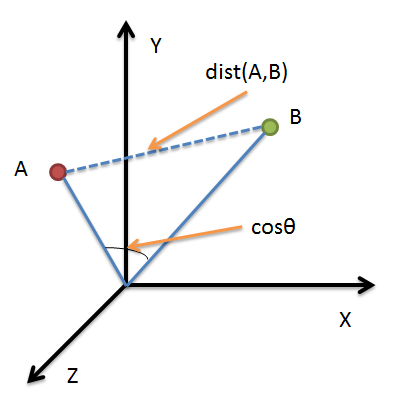
借助三维坐标系来看下欧氏距离和余弦相似度的区别:
从图上可以看出距离度量衡量的是空间各点间的绝对距离,跟各个点所在的位置坐标(即个体特征维度的数值)直接相关;而余弦相似度衡量的是空间向量的夹角,更加的是体现在方向上的差异,而不是位置。如果保持A点的位置不变,B点朝原方向远离坐标轴原点,那么这个时候余弦相似度cosθ是保持不变的,因为夹角不变,而A、B两点的距离显然在发生改变,这就是欧氏距离和余弦相似度的不同之处。
根据欧氏距离和余弦相似度各自的计算方式和衡量特征,分别适用于不同的数据分析模型:欧氏距离能够体现个体数值特征的绝对差异,所以更多的用于需要从维度的数值大小中体现差异的分析,如使用用户行为指标分析用户价值的相似度或差异;而余弦相似度更多的是从方向上区分差异,而对绝对的数值不敏感,更多的用于使用用户对内容评分来区分用户兴趣的相似度和差异,同时修正了用户间可能存在的度量标准不统一的问题(因为余弦相似度对绝对数值不敏感)。
The type of proximity measure should fit the type of data. For many types of dense, continuous data, metric distance measures such as Euclidean distance are often used. For sparse data, which often consists of asymmetric attributes, we typically employ similarity measures that ignore 0-0 matches, such as Consine, Jaccard.--Introduction to Data Mining.