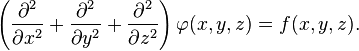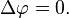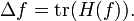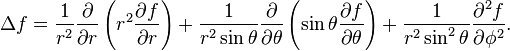泊松方程是数学中一个常见于静电学、机械工程和理论物理的偏微分方程。是从法国数学家、几何学家及物理学家泊松而得名的。 泊松方程为
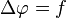
在这里 Δ 代表的是拉普拉斯算子，而 f 和 φ 可以是在流形上的实数或复数值的方程。 当流形属于欧几里得空间，而拉普拉斯算子通常表示为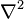 
，因此泊松方程通常写成
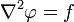
在三维直角坐标系，可以写成
如果没有f， 这个方程就会变成拉普拉斯方程
另外
在数学以及物理中， 拉普拉斯算子或是拉普拉斯算符（Laplace operator 或 Laplacian）是一个微分算子，通常写成 Δ 或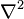 
；这是为了纪念皮埃尔-西蒙·拉普拉斯而命名的。
拉普拉斯算子有许多用途，此外也是椭圆型算子中的一个重要例子。
在物理中，常用于波方程的数学模型、热传导方程以及亥姆霍兹方程。
在静电学中，拉普拉斯方程和泊松方程的应用随处可见。在量子力学中，其代表薛定谔方程式中的动能项。
在数学中，经拉普拉斯算子运算为零的函数称为调和函数；拉普拉斯算子是霍奇理论的核心，并且是德拉姆上同调的结果。
[编辑] 定义
拉普拉斯算子是 n 维欧几里得空间中的一个二阶微分算子，定义为梯度（
）的散度（
）。因此如果 f 是二阶可微的实函数，则f的拉普拉斯算子定义为：
(1)
f 的拉普拉斯算子也是笛卡儿坐标系xi中的所有非混合二阶偏导数：
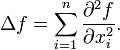(2)
作为一个二阶微分算子，拉普拉斯算子把 Ck 函数映射到 Ck-2 函数，对于k ≥ 2。表达式(1)（或(2)）定义了一个算子Δ : Ck(Rn) → Ck-2(Rn)，或更一般地，定义了一个算子Δ : Ck(Ω) → Ck-2(Ω)，对于任何开集Ω。
函数的拉普拉斯算子也是该函数的黑塞矩阵的迹：
坐标表示式
二维空间
- 其中x与y代表 x-y 平面上的笛卡儿坐标
- 另外极坐标的表示法为：
三维空间
- 笛卡儿坐标系下的表示法
- 圆柱坐标系下的表示法
- 球坐标系下的表示法
