什么是搜索算法
上一节介绍了图的基本概念,这一节介绍图的搜索算法。
图的搜索算法,最直观的理解就是从一个顶点到另一个顶点的路径。
最简单的是广度优先搜索和深度优先搜索,这也是这一节介绍的内容。另外还有A*、IDA*等启发式搜索算法。
本节内容以无向图为例,以下代码是图的代码实现。
// 无向图
class Graph
{
private int v; // 顶点个数
private LinkedList<int>[] adj; // 邻接表
public Graph(int v)
{
this.v = v;
adj = new LinkedList<int>[v];
for (int i = 0; i < v; i++)
{
adj[i] = new LinkedList<int>();
}
}
public void AddEdge(int s, int t)
{
// 无向图,一条边要存两次
adj[s].AddLast(t);
adj[t].AddLast(s);
}
}
广度优先搜索
广度优先搜索(Breadth-First-Search),简称BFS。一种“地毯式”的搜索策略,即先搜索跟起始点最近的顶点,慢慢往外扩散搜索。
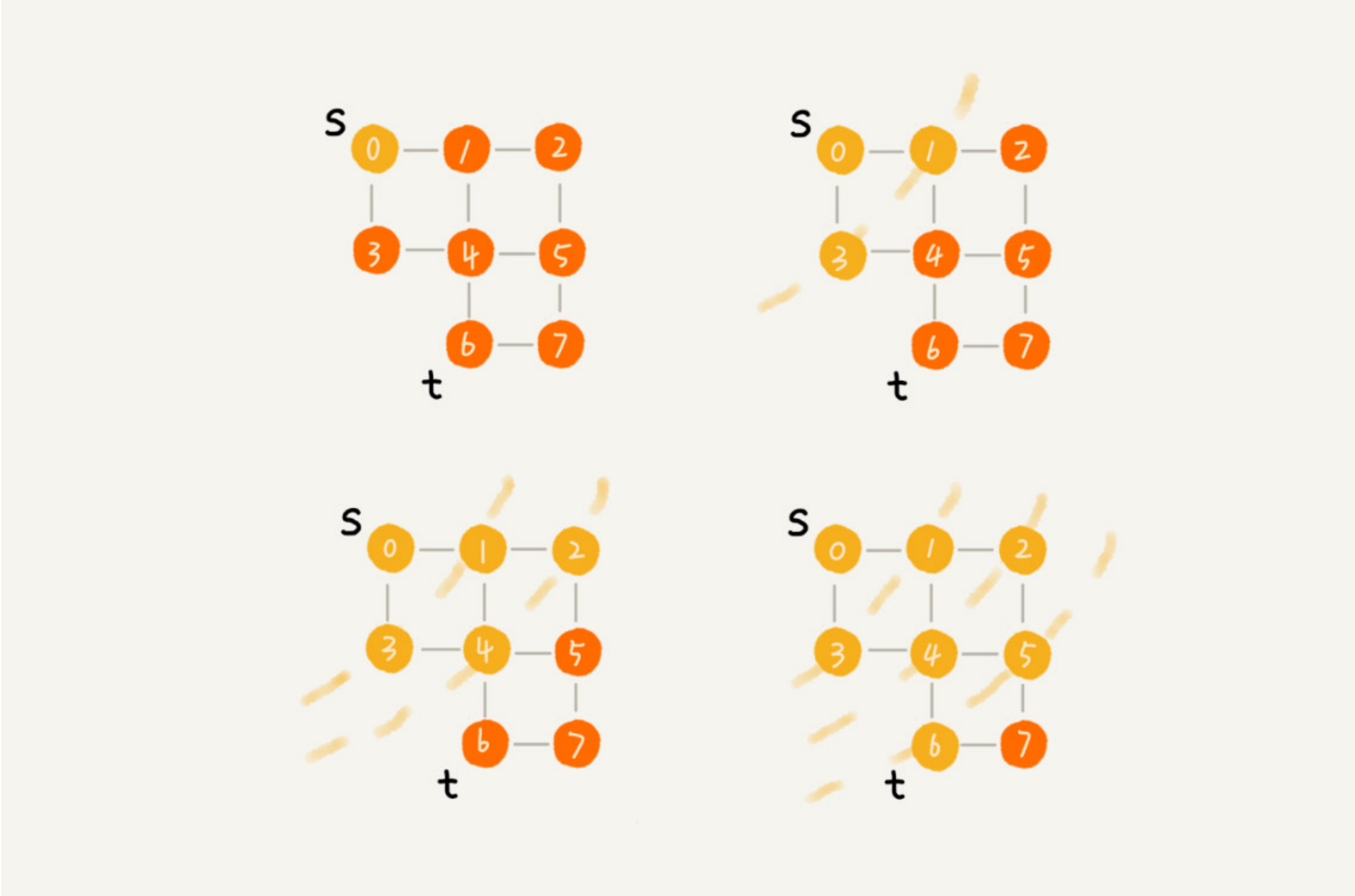
代码实现如下:
public void BFS(int s, int t)
{
if (s == t) return; // 起始点和终止点相同,直接返回。
Queue<int> queue = new Queue<int>(); //
bool[] visited = new bool[v]; // 用于记录顶点是否被访问过。
visited[s] = true;
int[] prev = new int[v]; // 记录当前顶点的前置顶点
for (int i = 0; i < v; i++)
{
prev[i] = -1;
}
queue.Enqueue(s);
while (queue.Count > 0)
{
// 下一层入队
int w = queue.Dequeue();
var head = adj[w].First;
while (head != null)
{
int q = head.Value;
if (!visited[q])
{
prev[q] = w;
if (q == t)
{
Print(prev, s, t);
return;
}
visited[q] = true;
queue.Enqueue(q);
}
head = head.Next;
}
}
}
private void Print(int[] prev, int s, int t)
{
if (prev[t] != -1 && t != s)
Print(prev, s, prev[t]);
Console.Write(t + " ");
}
通过下图来介绍BFS是如何执行的。
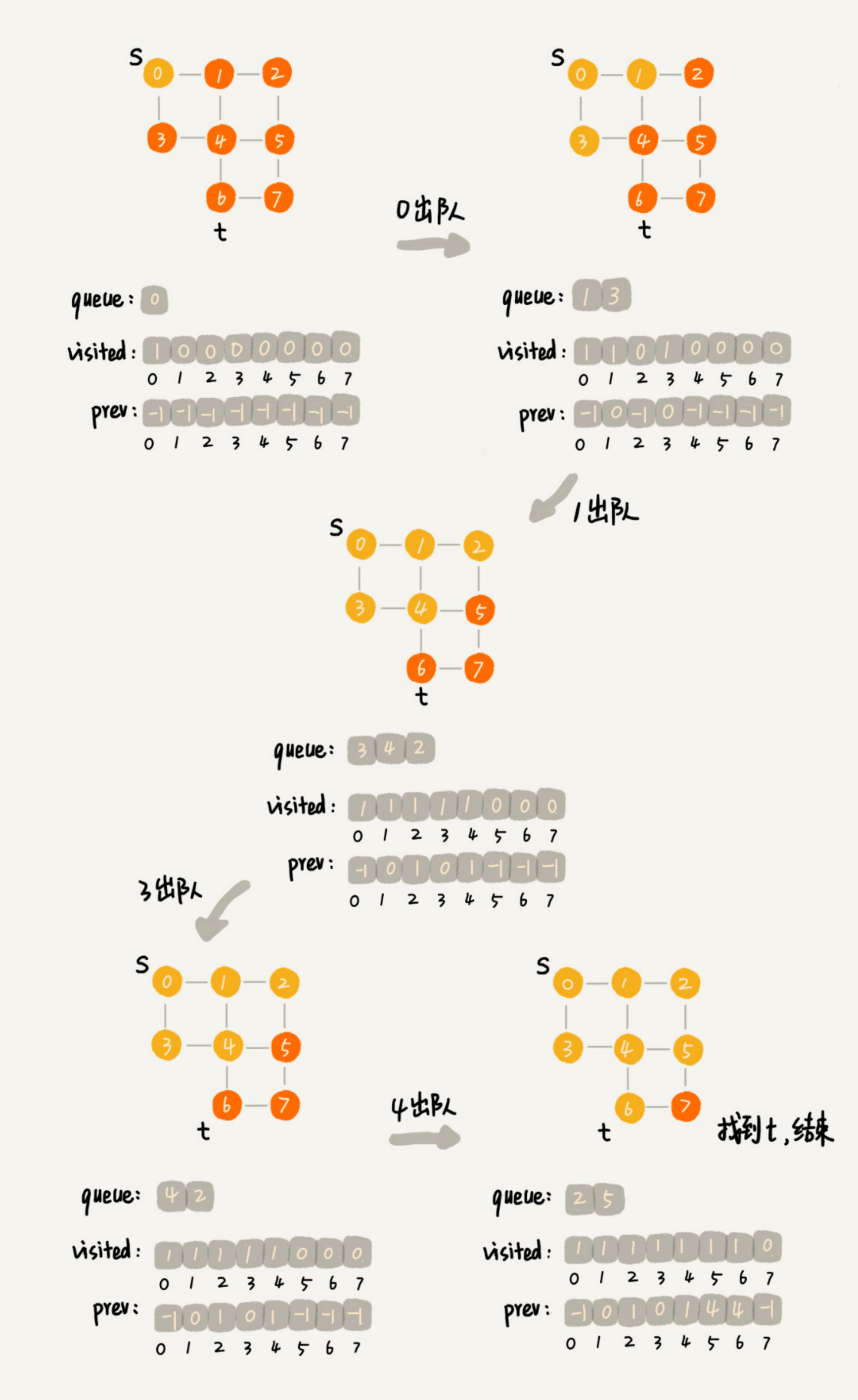
时间复杂度分析:
- 时间复杂度:O(E)。E表示图的边数
- 空间复杂度:O(V)。V表示图的顶点数
深度优先搜索
深度优先搜索(Depth-First-Search),简称DFS。最直观的例子是“走迷宫”,往最里面走,遇到分叉路先走一边然后再退回来走另一边,直到走到终点。
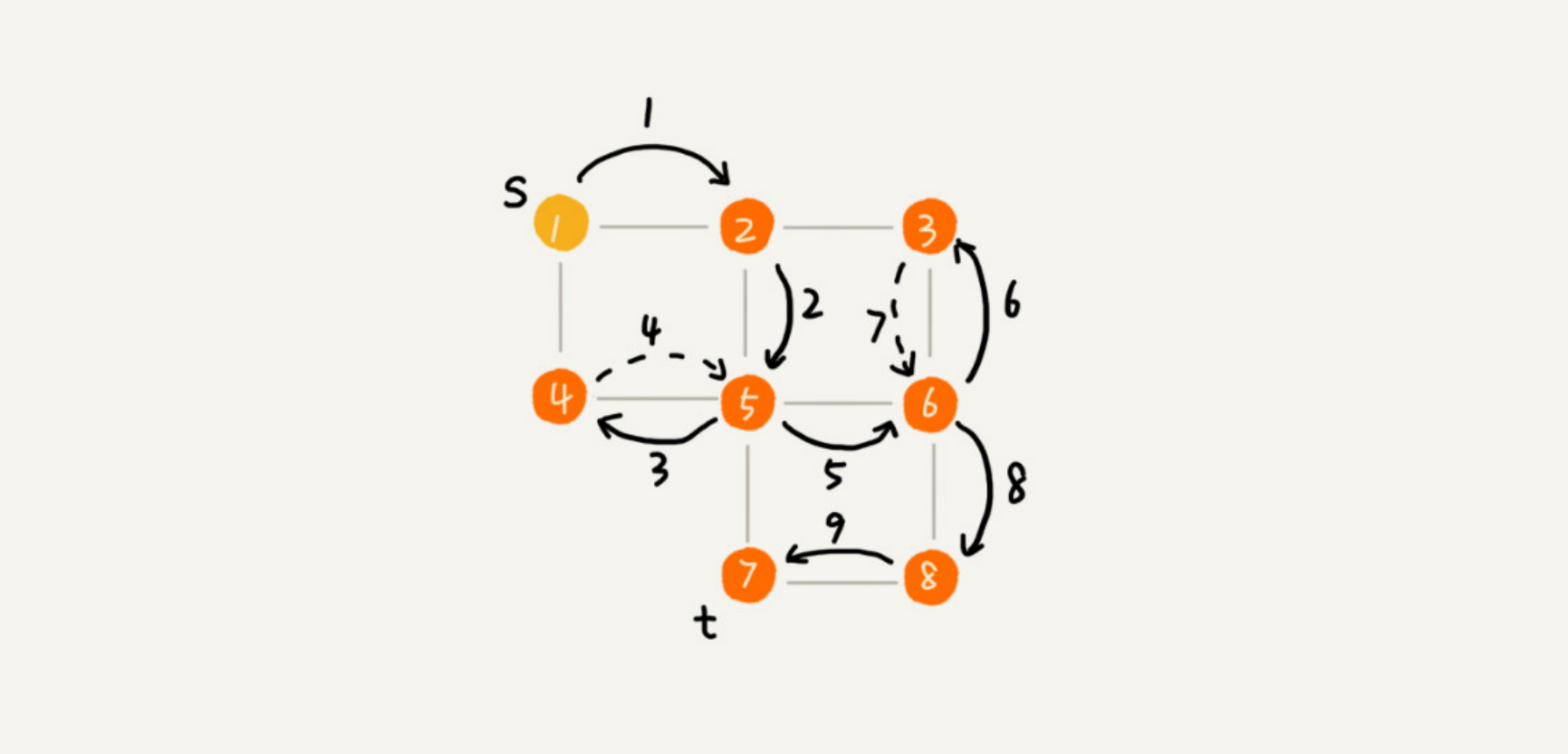
代码实现如下:
public void DFS(int s, int t)
{
found = false;
bool[] visited = new bool[v];
int[] prev = new int[v];
for (int i = 0; i < v; i++)
{
prev[i] = -1;
}
RecurDfs(s, t, visited, prev);
Print(prev, s, t);
}
private void RecurDfs(int w, int t, bool[] visited, int[] prev)
{
if (found) return;
visited[w] = true;
if (w == t)
{
found = true;
return;
}
var head = adj[w].First;
while (head != null)
{
int q = head.Value;
if (!visited[q])
{
prev[q] = w;
RecurDfs(q, t, visited, prev);
}
head = head.Next;
}
}
时间复杂度分析:
- 时间复杂度:O(E)。E表示图的边数
- 空间复杂度:O(V)。V表示图的顶点数
案例分析
如何找出社交网络中某个用户的三度好友关系?
社交网络可以用图来表示,找出某个用户的三度好友,即是从某个顶点(某个用户)走三步到达的顶点(三度好友)。
可使用BFS或DFS来实现,增加一个值来保存好友是第几度的,遍历过程里把度分别为1、2、3的顶点保存到结果集里。