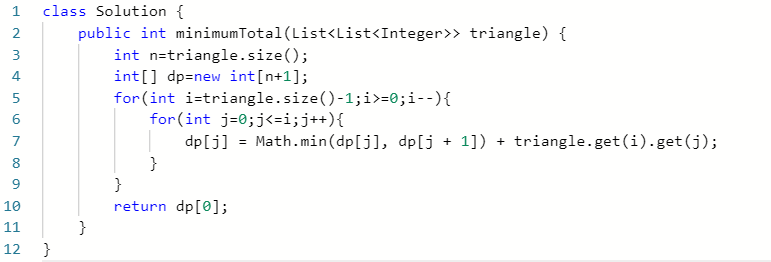
第120题:
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。来源:力扣(LeetCode)
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
1、像题目例子一样,一个三角形全部向左对齐就变成了一个等腰直角三角形;
因为直接暴力求解会浪费许多资源空间,所以可以定义一个二维数组dp[][]来存储下次需要的值,
例如dp[i][j]=min(dp[i-1][j],dp[i-1][j-1]),就是这个dp[i][j]的值一定第i-1行第j列的或者第i-1行第j-1列所存储的值加上集合t[i][j]的值
但是里面有一些特殊情况,
例如当j=0时,dp[i][0]只能等于dp[i-1][0]+t[i][0],因为这个格子的左上角并没有格子,他就是最左边的格子了;
例如当i=j时,dp[i][i]只能等于dp[i-1][i-1]+t[i][i],因为这个格子上面没有格子,这也就只有一种选择了;
其他位置的就和前面的公式算出来就可以,最终结果为dp数组内的最后一行的值的最小值。

2、对于等腰直角三角形里面的集合,可以用自底向上的方法来计算最小路径;
从第i-1行开始计算,这样最终得到的结果就是存储在最上面的唯一的一个格子里面dp[0]