矩形计数(rect)
Description
给出圆周上的 (N) 个点,请你计算出以这些点中的任意四个为四个角,能构成多少个矩 形。
点的坐标是这样描述的,给定一个数组 (v[1..N]),假设圆心为((0,0)),圆的周长 (C=sum_{i=1}^{N} v_i) ,第一个点坐标为((0,C/(2π)))。从第一个点开始,顺时针沿圆周走 (v_1) 个单位长度, 此时坐标为第二个点的坐标,再走 (v_2) 个单位长度,此时为第三个点的坐标,当走完 (v_1,v_2..v_i) 个距离后,为第 (i+1) 个点的坐标(全过程都是沿圆周顺时针)。特别的,走完 (v_1,v_2..v_n) 个 距离后,就会回到第一个点。
Input
输入文件名为(rect.in)
输入共 (N+1) 行。 第一行为正整数 (N)。 接下来 (N) 行每行一个正整数。其中第 (i+1) 行表示的是 (v_i)。
Output
输出文件名为(rect.out)
输出共(1) 行,一个整数,表示能构成的矩形的个数。
输入输出样例
(rect.in)
8
1
2
2
3
1
1
3
3
(rect.out)
3
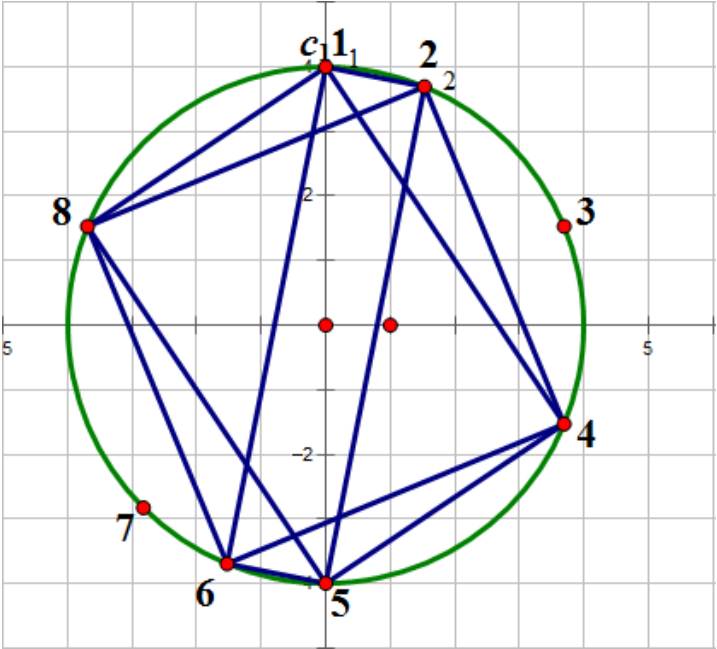
输入输出样例说明
很明显的是,圆中的矩形的对角线为圆的直径.
那么我们就可以对于圆的直径搞事情.
表示这个题的样例解释和题面对不上(但还是切了 (滑稽
直接计算圆的周长,(/2)就是"直径".(此处由于圆上的距离同样有(pi),因此这里忽略(pi))
手玩样例(观察)之后,我们发现,只要某一个点与另一个点之间的圆上距离也是(周长/2),那它们必然是被直径连接的.
代码
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cstring>
#include<cctype>
#define int long long
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int n,v[280],C,sum[280];
int cnt,dis[280][208];
int pipei[280];
bool ok[280][280];
bool judge(int i,int j)
{
if(pipei[i] and pipei[j] and !ok[i][j] and !ok[j][i] and !ok[pipei[i]][pipei[j]] and !ok[pipei[j]][pipei[i]])
if(dis[i][j]==dis[pipei[i]][pipei[j]] and pipei[i]!=j and pipei[j]!=i)
return true;
return false;
}
signed main()
{
//freopen("rect.in","r",stdin);
//freopen("rect.out","w",stdout);
in(n);
for(R int i=1;i<=n;i++)
in(v[i]),C+=v[i],sum[i+1]=sum[i]+v[i];
if(C&1){puts("0");return 0;}
C/=2;
for(R int i=1;i<=n;i++)
for(R int j=i+1;j<=n;j++)
{
int x=sum[j]-sum[i];
dis[i][j]=dis[j][i]=x;
if(x==C)pipei[i]=j,pipei[j]=i;
}
for(R int i=1;i<=n;i++)
for(R int j=i+1;j<=n;j++)
if(judge(i,j))
{
cnt++;
ok[i][j]=ok[j][i]=ok[pipei[i]][pipei[j]]=ok[pipei[j]][pipei[i]]=1;
}
printf("%lld",cnt);
fclose(stdin);
fclose(stdout);
return 0;
}
祖先(ancestor)
Description
任何一种生物的 DNA 都可以表示为一个由小写英文字母组成的非空字符串。科学家发 现,所有的生物都有可能发生变异。所谓变异,就是子代的 DNA 串与父代的 DNA 串有差 异。每次变异,DNA 串中恰好有一个字符会变成两个任意的字符。一共有 n 种可能的变异。 变异 ai->bici 表示字符 ai 有可能变异为两个字符 bici。详细来说,就是删掉一个字符 ai,之 后在原来 ai 的位置处,插入 bi,ci 两个字符(注意字符 bi 必须在 ci 的前面)。每种变异都 有可能发生任意多次。可以发现,每变异一次,DNA 串的长度会加 1。
如果有一种生物 a,他的 DNA 串是 s1,另外存在一种生物 b,他的 DNA 串是 s2。如 果 s2 可以通过若干次变异变为 s1,那么生物 b 就被叫做生物 a 的祖先。
现在,给定一种生物,他的 DNA 串是 s。请找出他的一个祖先,且这个祖先的 DNA 串 尽量短。
Input
输入文件 ancestor.in,共 n+2 行。
第一行包含一个非空字符串 s。
第二行含有一个整数 n,表示所有可能的变异。
接下来 n 行,每行描述一种可能的变异,按照 ai->bici 的格式。
s,ai,bi,ci 仅包含小写英文字母。
请注意:一种变异可能出现多次。
Output
输出文件名为 ancestor.out。
输出只有一行,一个整数,表示祖先 DNA 串的最短长度。
发现我们可以将字符两两合成,考虑区间(Dp)。
由于数据范围很小.
所以直接暴力预处理.
这里给出数组定义,看懂代码应该不是很难.
- (f[i][j][k])代表(i)到(j)能否合成字符(k)
- (dp[i][0])代表第(i)种变异,替换前的字符.
- (dp[i][1])代表第(i)种变异,替换后的第一个字符.
- (dp[i][2])代表第(i)种变异,替换后的第二个字符
- (ans[i][j])代表原串(i)到(j)替换成几个字符
注意预处理要倒叙,正序会出锅.(可以手玩一下.
代码
#include<cstdio>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<cstring>
#include<cctype>
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
char s[55],ss[55];
bool f[55][55][30];//f[i][j][k]代表从i到j能否为k
int dp[55][3],ans[55][55],len,n;
int main()
{
//freopen("ancestor.in","r",stdin);
//freopen("ancestor.out","w",stdout);
scanf("%s",s+1);len=strlen(s+1);
for(R int i=1;i<=len;i++)f[i][i][s[i]-'a']=true;
in(n);
for(R int i=1;i<=n;i++)
{
scanf("%s",ss+1);
dp[i][0]=ss[1]-'a';
dp[i][1]=ss[4]-'a';
dp[i][2]=ss[5]-'a';
}
// for(R int i=1;i<=n;i++)
// printf("%c->%c%c
",dp[i][0]+'a',dp[i][1]+'a',dp[i][2]+'a');
for(R int i=len;i>0;i--)
for(R int j=i+1;j<=len;j++)
for(R int k=i;k<j;k++)
for(R int o=1;o<=n;o++)
{
// printf("i:%d j:%d
",i,j);
if(f[i][k][dp[o][1]] and f[k+1][j][dp[o][2]])
{
// printf("i:%d j:%d %c
",i,j,dp[o][0]+'a');
f[i][j][dp[o][0]]=1;
}
}
for(R int i=1;i<=len;i++)
for(R int j=i+1;j<=len;j++)
ans[i][j]=2147483647;
for(R int i=len;i>0;--i)
for(R int j=i;j<=len;++j)
{
R bool flg=false;
for(R int k=0;k<26;++k)
if(f[i][j][k])
ans[i][j]=1,flg=true;
if(!flg)
for(R int k=i;k<j;++k)
ans[i][j]=min(ans[i][j],ans[i][k]+ans[k+1][j]);
}
printf("%d",ans[1][len]);
fclose(stdin);
fclose(stdout);
return 0;
}
Formula 1(f1)
Description
F1,中文全称为一级方程式锦标赛,是最高级的方程式赛车比赛,现在你作为一名选 手参加了一场 F1 的比赛,比较特殊地,本次比赛是在一个 N 个点 M 条边的无向图上举行 的。
起点是 S,终点是 T,每条边长度为 1 公里,赛车每行驶 1 公里耗油 1 个单位,途中共 有 k 个加油站,每经过加油站时,可以把油加满,但你的赛车设计顾问告诉你,油箱容量越 大,赛车跑的就越慢。为了追求最快的速度,在能顺利到达终点,不会中途没油的前提下, 你希望最小化油箱的容量(注意,虽然油箱变小可能导致路径变长,但我们只关心最小化的 油箱)。
Input
输入文件 f1.in。
第一行一个正整数 T 表示测试数据组数,每组数据格式如下:
第一行三个整数,N,M,K,表示无向图的点数,边数,加油站数。
第二行 K 个正整数 i1,i2..ik 表示这些点上有加油站(可能重复,保证至少一个加油站在 S 点)。
接下来 M 行,每行两个正整数 Bi,Ei 表示有一条连接(Bi,Ei)的双向边(可能有重边和自 环)。
最后一行两个正整数 S,T 表示起点、终点。
Output
输出文件名为 f1.out。
对于每组数据,如果没法到达终点,输出-1,否则输出最小化的油箱容量。
二分+(Spfa)题,表示第一眼没看出是二分 emmm(可能是思想太过拘泥了 emm
直接二分油箱容量即可.
这里(dis[i])代表到达(i)的剩余油量,到达一个加油站要加满.如果一个点不是加油站且没油了,直接(continue)
代码
#include<cstdio>
#include<cstdlib>
#include<cctype>
#include<queue>
#include<cstring>
#define clear(a,b) memset(a,b,sizeof a)
#define N 100008
#define R register
using namespace std;
inline void in(int &x)
{
int f=1;x=0;char s=getchar();
while(!isdigit(s)){if(s=='-')f=-1;s=getchar();}
while(isdigit(s)){x=x*10+s-'0';s=getchar();}
x*=f;
}
int T,n,m,k,dis[N],head[N],tot,s,t;
bool ok[N],vis[N];
struct cod{int u,v;}edge[N<<2];
inline void add(int x,int y)
{
edge[++tot].u=head[x];
edge[tot].v=y;
head[x]=tot;
}
inline bool spfa(int x)
{
for(R int i=1;i<=n;i++)dis[i]=-2147483647,vis[i]=false;
vis[s]=true;dis[s]=x;queue<int>q;
q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();vis[u]=false;
if(ok[u])dis[u]=x;
if(dis[u]==0)continue;
for(R int i=head[u];i;i=edge[i].u)
{
if(dis[edge[i].v]<dis[u]-1)
{
dis[edge[i].v]=dis[u]-1;
if(ok[edge[i].v])dis[edge[i].v]=x;
if(!vis[edge[i].v])
{
vis[edge[i].v]=true;
/ q.push(edge[i].v);
}
}
}
}
return dis[t]>=0;
}
int main()
{
//freopen("f1.in","r",stdin);
//freopen("f1.out","w",stdout);
in(T);
while(T--)
{
clear(ok,0);clear(head,0);tot=0;
int l=0,r=1e9,ans=214748364;
in(n),in(m),in(k);
for(R int i=1,x;i<=k;i++)in(x),ok[x]=true;
for(R int i=1,x,y;i<=m;i++)
{
in(x),in(y);
add(x,y);add(y,x);
}
in(s),in(t);
while(l<=r)
{
int mid=(l+r)>>1;
if(spfa(mid))r=mid-1,ans=mid;
else l=mid+1;
}
printf("%d
",ans==214748364?-1:ans);
}
fclose(stdin);
fclose(stdout);
return 0;
}