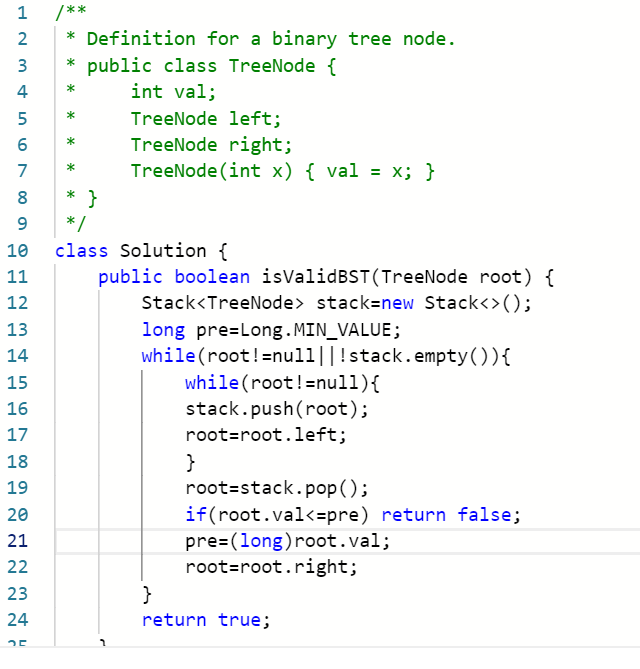
第94题:
给定一个二叉树,返回它的中序 遍历。(来自LeetCode)
1、对于一棵二叉树,除了可以利用递归来返回它的中序遍历外,还可以基于栈来遍历二叉树;
首先判断该树是否为空树,是的话返回空集合(list),不是则开始遍历;
当栈为空root不为空时,遍历没有结束,当栈不为空root为空时,遍历也没有结束,所以当栈为空或者root不为空时,都需要进行遍历操作;
当root不为空时,将root push入栈,然后指针指向它的左儿子节点,一直这样操作,直到root==null停止;
当指针指向最左边的叶子节点时,我们就可以将栈顶元素出栈,将这个元素的值add到list集合中;
然后再将root指向它的右子树,这里就回到了判断root和栈两者是否为空的时候;
如果这里只判断root==null的话,程序就会结束,但是此时栈内还有元素,所以这个地方判断就需要判断root和栈是否为空了。
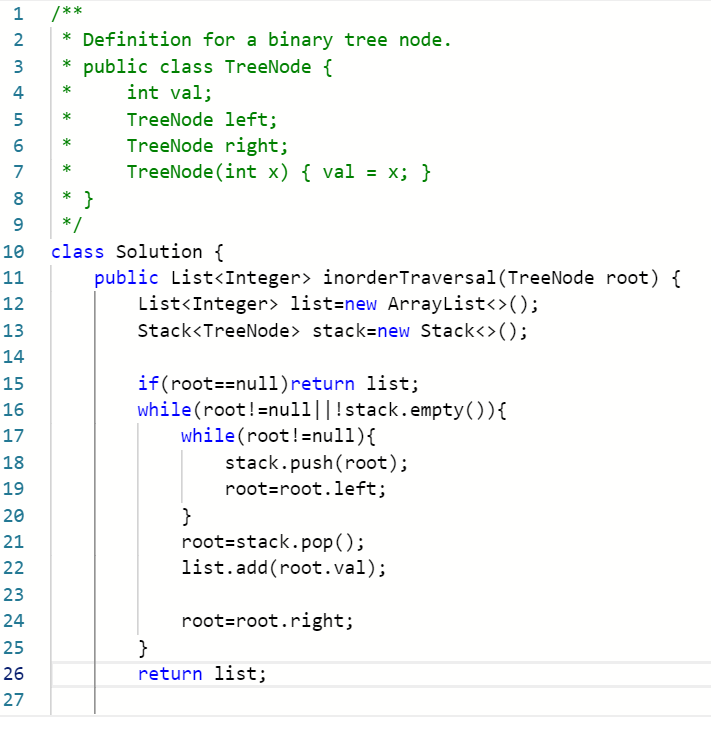
第98题:
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。来源:力扣(LeetCode)
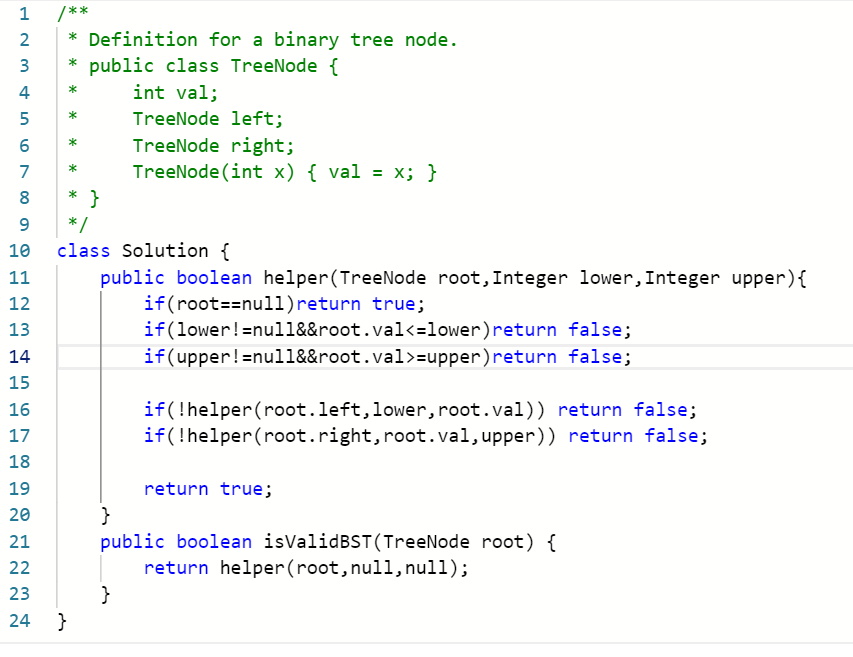
1、判断二叉树是否是一个有效的二叉搜索树,可以用到递归的方法;
首先判断该树是否为空,为空则返回true,它是一棵二叉搜索树;
如果不为空的话,那就开始递归判断了,二叉搜索树根节点的左儿子的值比根节点的值小,而根节点的右儿子的值比根节点的值大,而且他的左右儿子都必须是二叉搜索树;
在判断是否为二叉搜索树时,只需判断他的左儿子的值比它的值小,右儿子的值比它大就可以了;
这样就可以创建一个方法helper,先判断左孩子值是否小于根节点值,不是则返回false,在判断右孩子的值是否大于根节点值,不是则返回false;
然后再递归判断根节点的左儿子和右儿子是不是二叉搜索树,不是就返回false;
最后都成立的话就返回true。
2、由于二叉搜索树的中序遍历是一个递增的序列,所以我们可以利用在对二叉树进行中序遍历的过程中判断这个节点的值是否大于前一个节点的值,不是的话就返回false,是的话就返回true。