题目描述:

Input第一行两个整数N和M,为矩阵的边长。 第二行一个整数D,为豆子的总个数。 第三行包含D个整数V1到VD,分别为每颗豆子的分值。 接着N行有一个N×M的字符矩阵来描述游戏矩阵状态,0表示空格,#表示障碍物。而数字1到9分别表示对应编号的豆子。
Output仅包含一个整数,为最高可能获得的分值。
Sample Input
3 8 3
30 -100 30
00000000
010203#0
00000000
Sample Output
38
数据范围:
50%的数据满足1≤D≤3。
100%的数据满足1≤D≤9,1≤N, M≤10,-10000≤Vi≤10000。
思路分析:
我们一看到这么小的数据应该能想到要用DP,关键是怎么DP;
我们先说一下如何判断一个豆豆被围住,这需要用到“射线法”;
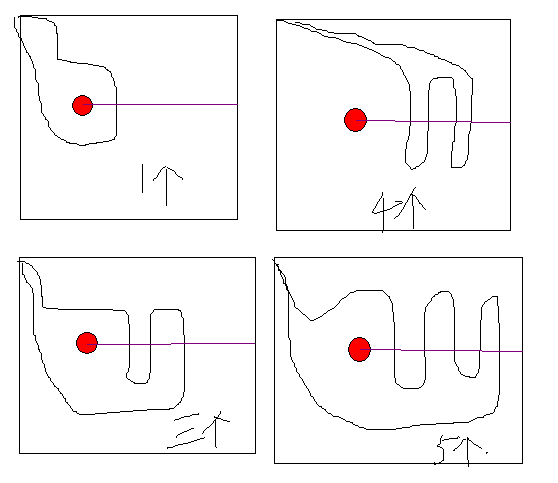
我们可以举几个例子来说,如上图所示(画得这么丑不要介意)我们发现,当从‘豆豆’向右延伸出一条直线时,如果与我们的路径有奇数个交点,那么豆豆将在路径所围成的圈内,否则在圈外,但还有一种特殊情况需要考虑:
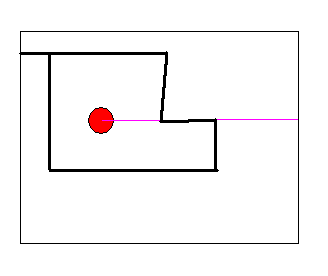
向右的直线和我们的路径有交时,会出现有偶数个交点(如图中)而在路径内的情况(我们计算交点数的方式是往下走时若过豆豆的纵坐标则记一次,所以中间横在紫线上的点不算,上图只有一左一右两个交点)
解决了判断的问题,我们便可以思考如何DP了
大致思路是,考虑Spfa的做法,从一个点出发,遍历所有与他相连的点,若合法则压入队内,一个点只走一次,知道队列为空,统计答案即可。如何找到与已知点相邻的点的坐标呢,我们在学栈时曾做过一道叫做细胞个数的题,我们可以从那里得到启发,即开两个数组,分别为
f1[4]={1,-1,0,0},f2[4]={0,0,1,-1},之后让已知点的坐标加上对应的值即可修改其位置。若i<2(即已知点上下移动),统计一下是否有点向右的直线与它有奇数个交点,有的话则在原来已知点的基础上加上这个豆豆的权值;我们用dp第一位和第二位表示点的坐标,第三位表示状态,如果一个点的一个状态合法(即vis为true,遍历过)则拿他和当前最大答案比较,最后输出最大答案。其他细节详见注释。
附上代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<queue> 5 #include<map> 6 using namespace std; 7 struct Node2{ //开一个结构体方便用队列存储 8 int x,y,dis; 9 Node2(int a,int b,int c){ 10 x=a;y=b;dis=c; 11 } 12 }; 13 int vis[11][11][1050],a[11][11],val[11]; 14 int n,m,cnt; 15 int dp[11][11][1050],x0[11],y0[11],ans=0; 16 //vis表示当前点当前状态是否计算过,val记录每个豆豆的权值, 17 //x0,y0分别存储豆豆的横,纵坐标,温馨提示:千万不要定义y1 18 //a数组记录棋盘,dp[i][j][k]记录坐标为(i,j)的点状态为k时权值. 19 int f1[4]={1,-1,0,0}; //用于已知点的移动 20 int f2[4]={0,0,1,-1}; 21 void Spfa(int x,int y){ 22 memset(vis,0,sizeof(vis)); //需要跑多次,记得初始化 23 memset(dp,0,sizeof(dp)); 24 dp[x][y][0]=0; 25 queue<Node2>q; 26 q.push(Node2(x,y,0)); 27 int tx,ty,tz,tdp,cross; 28 //tx,ty,tz表示新点的横,纵坐标及状态 29 //tdp表示当前状态权值,cross表示豆豆横坐标 30 while(!q.empty()){ 31 Node2 t=q.front();q.pop(); 32 for(int i=0;i<4;++i){ 33 tx=t.x+f1[i];ty=t.y+f2[i]; 34 if(tx<=0||ty<=0||tx>n||ty>m||a[tx][ty]!=0) //判断合法 35 continue; 36 tz=t.dis;tdp=dp[t.x][t.y][t.dis]-1;//由于又走了一步,分数要减一 37 if(i<2){ //判断是否加分 38 cross=min(tx,t.x); 39 for(int j=1;j<=cnt;++j){ 40 if(x0[j]!=cross||y0[j]>ty) //和豆豆的向右只限无交点 41 continue; 42 if(tz & (1<<(j-1))) tdp-=val[j]; //如果原来加过,再过一次时偶数变奇数,要减去 43 else tdp+=val[j]; //反之加上 44 tz=tz^(1<<(j-1)); //经过次数加一次 45 } 46 } 47 if(!vis[tx][ty][tz]){ //入队,准备下一次循环 48 dp[tx][ty][tz]=tdp; 49 q.push(Node2(tx,ty,tz)); 50 vis[tx][ty][tz]=1; 51 } 52 } 53 } 54 for(int i=0;i<(1<<cnt);++i) //统计当前点所有状态的答案 55 if(vis[x][y][i]) 56 ans=max(ans,dp[x][y][i]); 57 } 58 int main(){ 59 //freopen("a.txt","r",stdin); 60 scanf("%d%d%d",&n,&m,&cnt); 61 for(int i=1;i<=cnt;++i) 62 scanf("%d",&val[i]); 63 for(int i=1;i<=n;++i) 64 for(int j=1;j<=m;++j){ 65 char c=' '; 66 while(c==' '||c==' ') 67 scanf(" %c",&c); 68 if(c=='#') a[i][j]=-1; //构建棋盘 69 if(c>='0'&&c<='9'){ 70 x0[c-'0']=i;y0[c-'0']=j; //存储豆豆 71 a[i][j]=c-'0'; 72 } 73 } 74 for(int i=1;i<=n;++i) 75 for(int j=1;j<=m;++j){ 76 if(a[i][j]==0) 77 Spfa(i,j);//从每个点出发跑一遍 78 } 79 printf("%d ",ans); 80 return 0; 81 }
