题目描述
其精简之度令人发指
给出一个N个点的树,找出一个点来,以这个点为根的树时,所有点的深度之和最大
Input
给出一个数字N,代表有N个点.N<=1000000 下面N-1条边.
Output
输出你所找到的点,如果具有多个解,请输出编号最小的那个.
Sample Input
8 1 4 5 6 4 5 6 7 6 8 2 4 3 4
Sample Output
7
思路分析:
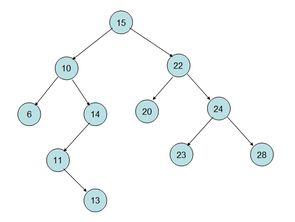
以上图为例,若以15号节点为根节点,则15号深度为0,22号节点深度为1(你要不习惯的话2也可以),24号为2,10号为1,14号为2;
若我们将根节点下移到十号,15号深度便变为了1,22号变为了2,24号变为了3,14号变为了1。
我们发现,从一个根节点开始,向它的一个子树移动之后,子树的点的深度全都减小了1,除此之外的点都增加了1,于是我们可以用一次DFS初始化出1号节点的深度总和,向它的一个子节点移动之后。以子节点为根的树的深度总和即为ans[v]=ans[u]+(n-siz[v])-siz[v];(ans[i]表示
以i为根时的深度总和,u为父节点,v为子节点,n为节点总数,siz[i]表示以i为根的子树大小),最后sort一下,输出即可.
附上代码

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 using namespace std; 5 const int N=2e6+10; 6 int n; 7 int Head[N],tot; 8 struct Node{ 9 int next,to; 10 }edge[N]; 11 void Add(int x,int y){ 12 edge[++tot].to=y; 13 edge[tot].next=Head[x]; 14 Head[x]=tot; 15 } 16 long long depth[N],siz[N]; 17 void dfs1(int u,int fa,int t){ //初始化siz数组,同时计算以1 18 depth[u]=t; //为根时的深度总和 19 siz[u]=1; 20 for(int i=Head[u];i;i=edge[i].next){ 21 int v=edge[i].to; 22 if(v==fa) continue; 23 dfs1(v,u,t+1); 24 siz[u]+=siz[v]; 25 depth[u]+=depth[v]; 26 } 27 } 28 struct o{ 29 long long depth,id; //便于sort后输出编号 30 bool operator < (const o& a) const{ 31 if(a.depth==depth) return a.id>id; 32 return a.depth<depth; 33 } 34 }ans[N]; 35 void dfs2(int u,int fa){ 36 ans[u].id=u; 37 if(u!=1) ans[u].depth=ans[fa].depth+n-2*siz[u]; //原来的式子化简了一下 38 for(int i=Head[u];i;i=edge[i].next){ 39 int v=edge[i].to; 40 if(v==fa) continue; 41 dfs2(v,u); 42 } 43 } 44 int main(){ 45 scanf("%d",&n); 46 for(int i=1;i<n;++i){ 47 int x,y; 48 scanf("%d%d",&x,&y); 49 Add(x,y);Add(y,x); 50 } 51 dfs1(1,0,0); 52 ans[1].depth=depth[1]; //给1的深度和赋初值 53 dfs2(1,0); 54 sort(ans+1,ans+1+n); 55 printf("%lld ",ans[1].id);//记得开long long 56 return 0; 57 }
