Codeforces Round #466 (Div. 2)F. Machine Learning 离散化+带修改的莫队

题目链接：http://codeforces.com/contest/940/problem/F

F. Machine Learning

time limit per test

4 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

You come home and fell some unpleasant smell. Where is it coming from?

You are given an array a. You have to answer the following queries:

1. You are given two integers l and r. Let ci be the number of occurrences of i in al: r, where al: r is the subarray of a from l-th element to r-th inclusive. Find the Mex of {c0, c1, ..., c109}
2. You are given two integers p to x. Change ap to x.

The Mex of a multiset of numbers is the smallest non-negative integer not in the set.

Note that in this problem all elements of a are positive, which means that c0 = 0 and 0 is never the answer for the query of the second type.

Input

The first line of input contains two integers n and q (1 ≤ n, q ≤ 100 000) — the length of the array and the number of queries respectively.

The second line of input contains n integers — a1, a2, ..., an (1 ≤ ai ≤ 109).

Each of the next q lines describes a single query.

The first type of query is described by three integers ti = 1, li, ri, where 1 ≤ li ≤ ri ≤ n — the bounds of the subarray.

The second type of query is described by three integers ti = 2, pi, xi, where 1 ≤ pi ≤ n is the index of the element, which must be changed and 1 ≤ xi ≤ 109 is the new value.

Output

For each query of the first type output a single integer  — the Mex of {c0, c1, ..., c109}.

Example

input

Copy

10 4
1 2 3 1 1 2 2 2 9 9
1 1 1
1 2 8
2 7 1
1 2 8

output

2
3
2

Note

The subarray of the first query consists of the single element — 1.

The subarray of the second query consists of four 2s, one 3 and two 1s.

The subarray of the fourth query consists of three 1s, three 2s and one 3.

题解：因为a[i]的值范围有1e9,但操作的数不会超过2e5,离散化的到对应值的大小。然后用带修改莫队算法，复杂度 .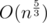

没学过莫队的可以看这个.

#include<bits/stdc++.h>
#include<set>
#include<iomanip>
#include<iostream>
#include<string>
#include<cstring>
#include<algorithm>
#define pb push_back
#define ll long long
#define PI 3.14159265
#define ls l,m,rt<<1
#define rs m+1,r,rt<<1|1
#define eps 1e-7
typedef unsigned long long ull;
const int mod=1e9+9;
const ll inf=0x3f3f3f3f3f3f3f;
const int maxn=1e5+50;
using namespace std;
int a[maxn],belong[maxn],block,ans=1,l=1,r=0,an[maxn],n,qq,cnt,cn[2*maxn],c[maxn];
struct que
{
    int l,r,tim,id;
}q[maxn];
struct cha
{
    int p,now,old;
}st[maxn];
int num[2*maxn];
bool cmp(que a,que b)
{
    return belong[a.l]==belong[b.l]?belong[a.r]==belong[b.r]?a.tim<b.tim:a.r<b.r:a.l<b.l;
}
void add(int p,int d)
{

    c[cn[p]]--;
    cn[p]+=d;
    c[cn[p]]++;
}
void slove(int p,int x)
{
   if(p>=l&&p<=r)
   {
        add(a[p],-1);
        add(x,1);
   }
   a[p]=x;
}
int main()
{

    scanf("%d %d",&n,&qq);
    //block=sqrt(n);
    block=pow(n,0.666666);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        num[cnt++]=a[i];
        belong[i]=i/block+1;
    }
    int T=0,t=0;
    while(qq--)
    {
        int op,L,R;
        scanf("%d %d %d",&op,&L,&R);
        if(op==1)
        {
            q[++t]=(que){L,R,T,t};
        }
        else
        {
            st[++T]=(cha){L,R,a[L]};
            num[cnt++]=R;
            a[L]=R;
        }
    }
    sort(num,num+cnt);
    sort(q+1,q+t+1,cmp);
    int sz=unique(num,num+cnt)-num;
    for(int i=1;i<=n;i++)
    {
        a[i]=lower_bound(num,num+sz,a[i])-num;
    }
    for(int i=1;i<=T;i++)
    {
        st[i].now=lower_bound(num,num+sz,st[i].now)-num;
        st[i].old=lower_bound(num,num+sz,st[i].old)-num;
    }
    for(int i=1;i<=t;i++)
    {
        while(T<q[i].tim){slove(st[T+1].p,st[T+1].now);T++;}
        while(T>q[i].tim){slove(st[T].p,st[T].old);T--;}

        while(l<q[i].l){add(a[l],-1);l++;}
        while(l>q[i].l){add(a[l-1],1);l--;}
        while(r<q[i].r){add(a[r+1],1);r++;}
        while(r>q[i].r){add(a[r],-1);r--;}

        while(c[ans])ans++;
        an[q[i].id]=ans;
        ans=1;
    }
    for(int i=1;i<=t;i++)
    {
        printf("%d
",an[i]);
    }
    return 0;
}