Memory and his friend Lexa are competing to get higher score in one popular computer game. Memory starts with score a and Lexa starts with score b. In a single turn, both Memory and Lexa get some integer in the range [ - k;k] (i.e. one integer among - k, - k + 1, - k + 2, ..., - 2, - 1, 0, 1, 2, ..., k - 1, k) and add them to their current scores. The game has exactly t turns. Memory and Lexa, however, are not good at this game, so they both always get a random integer at their turn.
Memory wonders how many possible games exist such that he ends with a strictly higher score than Lexa. Two games are considered to be different if in at least one turn at least one player gets different score. There are (2k + 1)2t games in total. Since the answer can be very large, you should print it modulo 109 + 7. Please solve this problem for Memory.
The first and only line of input contains the four integers a, b, k, and t (1 ≤ a, b ≤ 100, 1 ≤ k ≤ 1000, 1 ≤ t ≤ 100) — the amount Memory and Lexa start with, the number k, and the number of turns respectively.
Print the number of possible games satisfying the conditions modulo 1 000 000 007 (109 + 7) in one line.
1 2 2 1
6
1 1 1 2
31
2 12 3 1
0
In the first sample test, Memory starts with 1 and Lexa starts with 2. If Lexa picks - 2, Memory can pick 0, 1, or 2 to win. If Lexa picks - 1, Memory can pick 1 or 2 to win. If Lexa picks 0, Memory can pick 2 to win. If Lexa picks 1 or 2, Memory cannot win. Thus, there are3 + 2 + 1 = 6 possible games in which Memory wins.
题意:两个人最开始有a,b两个初始数,玩t轮游戏,每个人都随机从【-k,k】之间获得一个数加进他们的分数,问最后问最开始是a的人比另外一个大的方案数%1e9就可以;
题解:f[i]表示得分为i的情况数(每轮更新),然后用sum[]来维护f[i]的前缀和,状态转移方程就是f[j]=(sum[loc]-sum[j-k-1]+mod)%mod;(loc=min(j+k,r-k)注意边界)
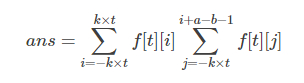
然后就是数组下表不能小于0;
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #define ll long long double eps=1e-7; const int maxn=4e5+2000; int zero=2e5+2005; const int mod=1e9+7; using namespace std; int f[maxn],sum[maxn]; int a,b,k,t; int main() { scanf("%d %d %d %d",&a,&b,&k,&t); int l=zero-k,r=zero+k; //if(a==1&&b==100&&k==1000&&t==100) for(int i=l;i<=r;i++) { f[i]=1; sum[i]=sum[i-1]+f[i]; } for(int i=2;i<=t;i++) { l=zero-k*i,r=zero+k*i; for(int j=l;j<=r;j++) { int loc=min(j+k,r-k); f[j]=(sum[loc]-sum[j-k-1]+mod)%mod; } for(int j=l;j<=r;j++) { sum[j]=(sum[j-1]+f[j])%mod; } } l=zero-t*k; r=zero+t*k; int ans=0; for(int i=l;i<=r;i++) { int loc=min(i+a-b-1,r); ans=(ans+((ll)sum[loc]*f[i])%mod)%mod; } printf("%d ",ans); }