41 KMP子串查找算法
原文:https://www.cnblogs.com/wanmeishenghuo/p/9671794.html参考狄泰软件相关教程
问题:


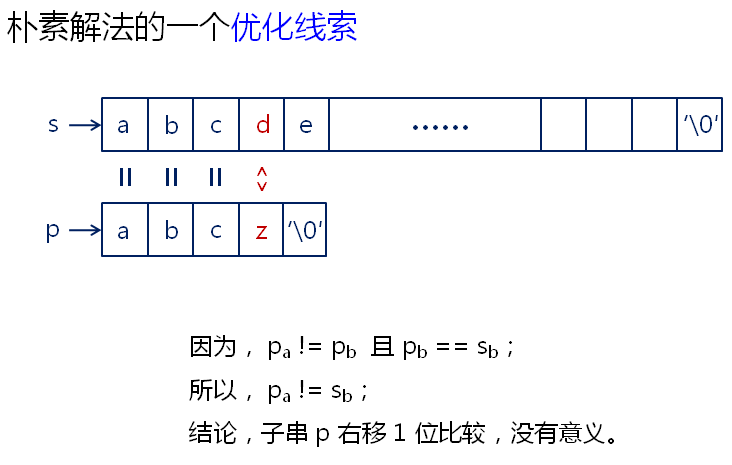
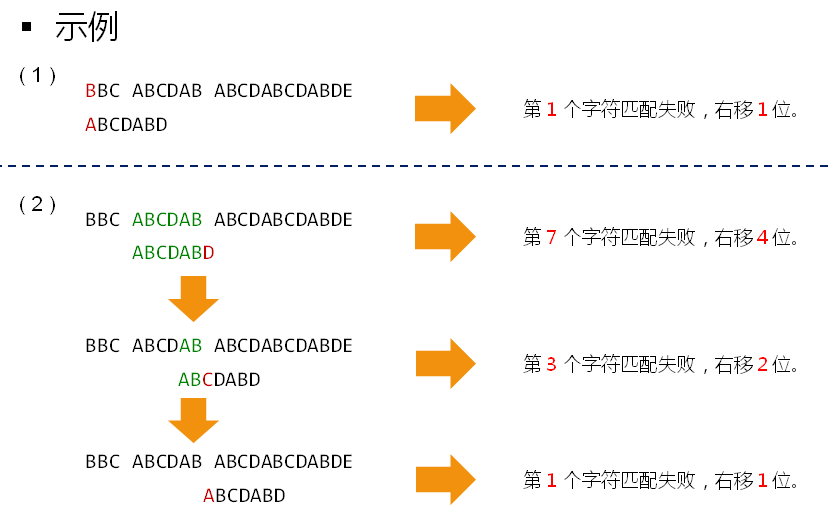
右移的位数和目标串没有多大的关系,和子串有关系。

已匹配的字符数现在已经有了,部分匹配值还没有。

前六位匹配成功就去查找PMT中的第六位。
现在的任务就是求得部分匹配表。
问题:怎么得到部分匹配表呢?


前缀集合和后缀集合取最长的交集就是部分匹配值。
例如,上图中前缀和后缀没有交集,部分匹配值就是0。

问题:
怎么编程产生部分匹配表呢?

从第2个字符开始递推,做一个贪心的假设,我们现在要求的匹配值是由上一次得到的匹配值加1得到。
假设有5个字符,当前的匹配值是3,当有6个字符时,我们就假设匹配值是4。
推导过程:

ll值定义为前缀和后缀交集元素的最大长度。
第一个元素的ll值为0。
当前要求的ll是以历史的ll值求出来的。
当可选的ll值为0时,直接比对首尾元素,若不相等则为0,若相等则为1。
例如:
ab的ll值为0,当向后扩展一个字符求aba的ll值时,需要根据ab的ll值来求,
因为ab的ll值为0,我们只需要比对aba中的第一个a和最后一个a,发现相等,于是aba的ll值为1。
再向后扩展一个字符abab,这时候上一个ll值不为零,我们就以上次匹配的字符a为种子,向后扩展比较,第一个a向后扩展一下为ab,
第三个a向后扩展一下为ab,a和a比较相等(这个已经比对过),b和b比较相等,于是abab的ll值为1+1=2。
再向后扩展一个字符ababa,上一个ll值不为0,我们以ab为种子,分别向后扩展一个字符,得到aba(前三个)和aba(后三个),
ab和ab已经比对过了,于是只需要比对最后一个a和a,发现相等,于是ll值为2+1=3。
再向后扩展一个字符ababax,上一个ll值不为0,现在分别以aba为种子向后扩展一个字符,得到abab(前四个)和abax(后四个),
aba和aba刚才已经比对过,现在比较b和x发现不相等,于是,为了还能扩展,我们需要在abc中找一个种子继续扩展看一下,
如上图中两个画红圈的a,这就是aba的前缀和aba的后缀的最大交集,这两个aba是方框中的aba,一个是aba(1-3),一个是aba(3-5)。
于是,我们需要aba的最大匹配值,我们去查找aba这个字符串的最大匹配值,这个刚才已经求得了,
查PMT[3]即可,aba的ll值为1,于是以第一个a和第五个a为种子,分别向后扩展一个字符,得到ab和ax,a和a已经比对过,
现在比较b和x发现不相等,于是再去查a这个字符串的匹配值,我们也已经求出来了是0,因为a的ll值为0,所以我们直接比对首尾
元素,于是比较第一个a和最后一个元素x,发现不相等,于是ababax的ll值为0。
上面abab和abax匹配不上时,我们直接查找的PMT[3],而略过了PMT[2],这是为什么呢?
假设可选的ll值为2,这时前缀就是ab,后缀就是ba,然后以这里的前后缀作为种子来扩展,这时可以看出,不用扩展就可以知道,
肯定不会匹配,因为ab和ba就匹配不上,为什么ll值为2就是不对呢?
因为要使得有相同的前缀和后缀进行扩展,必然的要去前缀和后缀元素的交集的最大长度,aba和aba前缀、后缀交集的最大长度就是aba的ll值,因此,只能拿a来进行扩展。
编程实现:
#include <iostream>
#include <cstring>
#include "DTString.h"
using namespace std;
using namespace DTLib;
int* make_pmt(const char* p)
{
int len = strlen(p);
int* ret = static_cast<int*>(malloc(sizeof(int) * len));
if( ret != NULL )
{
int ll = 0;
ret[0] = 0; // 第0个元素(长度为1的字符串)的ll值为0
for(int i = 1; i < len; i++)
{
//不成功的情况
while( (ll > 0) && (p[ll] != p[i]) )
{
ll = ret[ll];
}
// 假设最理想的情况成立
//在前一个ll值的基础行进行扩展,只需比对最后扩展的字符是否相等
//相等的话ll值加1,并写入到部分匹配表
if( p[ll] == p[i] )
{
ll++;
}
ret[i] = ll; // 将ll值写入匹配表
}
}
return ret;
}
int main()
{
int* pmt = make_pmt("ababax");
for(int i = 0; i < strlen("ababax"); i++)
{
cout << i << ":" << pmt[i] << endl;
}
return 0;
}
结果如下:

测试程序2:
#include <iostream>
#include <cstring>
#include "DTString.h"
using namespace std;
using namespace DTLib;
int* make_pmt(const char* p)
{
int len = strlen(p);
int* ret = static_cast<int*>(malloc(sizeof(int) * len));
if( ret != NULL )
{
int ll = 0;
ret[0] = 0; // 第0个元素(长度为1的字符串)的ll值为0
for(int i = 1; i < len; i++)
{
//不成功的情况
while( (ll > 0) && (p[ll] != p[i]) )
{
ll = ret[ll];
}
// 假设最理想的情况成立
//在前一个ll值的基础行进行扩展,只需比对最后扩展的字符是否相等
//相等的话ll值加1,并写入到部分匹配表
if( p[ll] == p[i] )
{
ll++;
}
ret[i] = ll; // 将ll值写入匹配表
}
}
return ret;
}
int main()
{
int* pmt = make_pmt("ABCDABD");
for(int i = 0; i < strlen("ABCDABD"); i++)
{
cout << i << ":" << pmt[i] << endl;
}
return 0;
}
结果如下:

KMP子串查找算法:
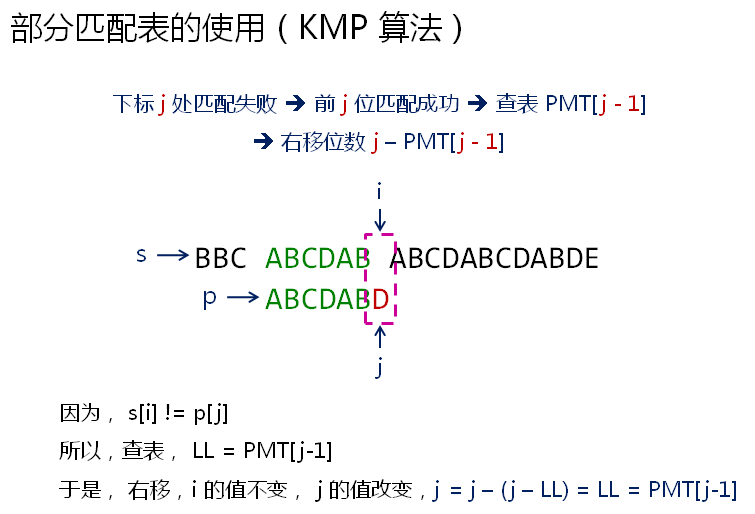
j为6时不匹配,前j位匹配成功,查PMT[j-1],得出右移位数 j - PMT[j - 1],也就是 j - LL,子串ABCDABD右移 j - LL位之后,j的值就变为 j - (j - LL),即LL。
程序如下:
#include <iostream>
#include <cstring>
#include "DTString.h"
using namespace std;
using namespace DTLib;
int* make_pmt(const char* p) // O(m)
{
int len = strlen(p);
int* ret = static_cast<int*>(malloc(sizeof(int) * len));
if( ret != NULL )
{
int ll = 0;
ret[0] = 0; // 第0个元素(长度为1的字符串)的ll值为0
for(int i = 1; i < len; i++)
{
//不成功的情况
while( (ll > 0) && (p[ll] != p[i]) )
{
ll = ret[ll];
}
// 假设最理想的情况成立
//在前一个ll值的基础行进行扩展,只需比对最后扩展的字符是否相等
//相等的话ll值加1,并写入到部分匹配表
if( p[ll] == p[i] )
{
ll++;
}
ret[i] = ll; // 将ll值写入匹配表
}
}
return ret;
}
int kmp(const char* s, const char* p) //O(m) + O(n) = O(m + n)
{
int ret = -1;
int sl = strlen(s);
int pl = strlen(p); //子串
int* pmt = make_pmt(p); //O(m)
if( (pmt != NULL) && (0 < pl) && (pl <= sl))
{
for( int i = 0,j = 0; i < sl; i++ )
{
while( (j > 0) && (s[i] != p[j]) ) // j小于等于0时要退出
{
j = pmt[j];
}
if( s[i] == p[j] )
{
j++;
}
if( j == pl ) // j的值如果最后就是子串的长度,意味着查找到了
{
ret = i + 1 - pl; // 匹配成功时i的值停在最后一个匹配的字符上
break;
}
}
}
free(pmt);
return ret;
}
int main()
{
cout << kmp("abcde", "cde") << endl;
cout << kmp("ababax", "ba") << endl;
cout << kmp("ababax", "ax") << endl;
cout << kmp("ababax", "") << endl;
cout << kmp("ababax", "ababax") << endl;
cout << kmp("ababax", "ababaxy") << endl;
return 0;
}
KMP具有线性时间复杂度,最朴素的算法的时间复杂度是O(m*n)。
第69行的计算图解如下:

程序运行结果如下:
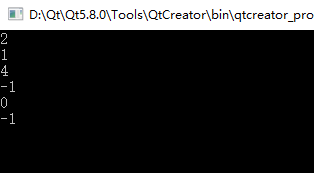
小结:
