为了准备数学建模的比赛，我在网上学习了几种建模算法，当然这里有很多是从一些博客神那里学到的，加上了一点自己的理解，，在此真心感谢那些分享的大神。
算法一：层次分析法，
首先要明确层次分析法可以解决那些问题，顾名思义这里的层次可以理解为不同的影响因素，例如影响粮食价格的因素，影响手机市场的因素。就是在分析这些因素对于结果的影响程度通过最后得出的结果来做决策，是提供方案和措施的算法。这是个人在分析数学建模优秀论文得出的结论（自己的理解而已）。
一、对于此算法的权威定义：
层次分析法根据问题的性质和要达到的总目标，将问题分解为不同的组成因素，并按照因素间的相互关联影响以及隶属关系将因素按不同层次聚集组合，形成一个多层次的分析结构模型，从而最终使问题归结为最底层（供决策的方案、措施等）相对于最高层（总目标）的相对重要权重的确定或相对优劣次序的排定。
其中：最高层：决策的目的、要解决的问题
最底层：决策时的备选方案
中间层：考虑的因素、决策的准则。
在深入了解层次分析法之前，需要做一个准备工作，了解什么是矩阵一致法。
二、一致矩阵法
通俗点说，假如现在有可以让我选择的几个地方去旅游，分别是桂林、张家界、青岛、三亚，而我想去的地方的主次是：三亚>张家界>桂林>青岛，怎么把你的这种意愿转化为数学模型让大家接收呢，或者说量化你的意愿程度呢？就是一致矩阵
一致矩阵法的核心思想有两个：
- 不把所有的因素放在一起比较，而是两两互相比较
- 采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。
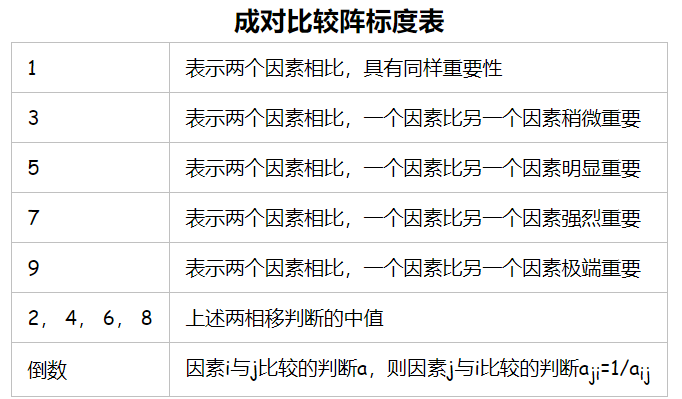
核心思想和这个表是什么意思呢，好还是旅游的那个例子，设：
| 桂林 | 张家界 | 青岛 | 三亚 |
| A1 | A2 | A3 | A4 |
根据矩阵一直的思想我需要创建一个4X4jdm.com的矩阵
| A1 | A2 | A3 | A4 | |
| A1 | 1 | 3 | 5 | 7 |
| A2 | 1/3 | 1 | 3 | 5 |
| A3 | 1/5 | 1/3 | 1 | 3 |
| A4 | 1/7 | 1/5 | 1/3 | 1 |
在根据我们的主观意识给这个矩阵填好相应的系数后，再根据倒数规则补充剩下的空格。就能完成我们这个一致性矩阵。
也许大家会讲，那这个主观意识很重要诶。是的没错，层次分析法其实就是一种比较主观的方法。所以，在填入你所需要的标度数时，尽量查阅多一些文献，这样结果会更加准确。
层次分析法：
问题：【选择旅游地】如何在3个目的地按照景色、费用、居住条件等因素进行选择。
解法：
1.首先，在这个问题中，我们要解决的问题就是选择旅游地，不妨设为Z，这就是我们的最高层 = Z；
2.接着，在题目中，我们旅游地的可选择只有三个，分别设为B1，B2，B3。这就是我们的最底层；
3.最后就是我们的中间层，根据定义，中间层就该是景色、费用、居住、饮食、旅途这些条件，分别设为A1，A2，A3，A4，A5。
接下来我们就开始构建层次模型吧。如下图所示
大家这时候应该体会到了层次分析法是什么样的一种方法了吧。如果这时还不明白的请看回官方定义。
好了，也就是，通过计算出各个层之间的权重，根据权重来得出我们要的结果。，这就需要我们列出5个3X3de一致性矩阵，计算出数值最大的，就是我们要去的地方。
醉的问题模型，是摘取的一个大V的，他讲的很好，附上他的博客地址：https://www.cnblogs.com/Qling/p/9289580.html，希望大家去看看。