前言
在计算机内采用二进制0,1可以存储数字,文字,图片,视频等。本文讲解的是计算机数字中整数的存储。关于整数的表示,计算机有三种编码方式表达,分别是原码,反码和补码。计算机中对于整数的存储是其补码。文章首先解释原码,反码,补码是什么,最后解释为什么存储的是补码。
原码
正数的原码是其本身的二进制数,然后符号位为0.如:25等于二进制的 0001 1001 .负数的原码是它的绝对值的二进制数,然后符号位为1。如:-25等于二进制的 1001 1001。
ps:如果是用8位来表示一个数字,符号位就是第8位,用32位来表示一个数字,符号位就是第32位。符号位就是二进制数的最高位,它用来标记数字的正负,正为0,负为1。
反码
正数的反码就是它的原码,如25的反码就是 0001 1001。负数的反码是它的原码除了符号位不变,其他各个位数取反,即0变1,1变0. 如 -25的反码: 1110 0110 (原码: 1001 1001)
补码
正数的补码就是它的原码,如25的补码就是 0001 1001。负数的补码是它的反码加1。如-25的补码: 1110 0111 (反码: 1110 0110)
为什么存储的是补码
首先明白一点,减法操作的复杂度是比加法的复杂度是要高的,因为它涉及到借位,例如:25-18 ,5-8肯定不够减,它就需要向十位借个10来相减。这样无疑降低了计算机的计算运行速度。这时我们可以想到,无论是减法操作还是加法操作可以统一看作加法操作,25-18可以看作 25+(-18)。这里我们模拟计算机采用原码的方式进行计算

(原码方式相加)
二进制1010 1011转换为十进制等于 -43 ,这个答案和正确的计算结果7相差太远了。我们再来思考一下,25-18可以看作 25-18+99+1-100。也等于(99-18+1)+25-100。在十进制中,99是最大的两位数,在二进制中用8位表示一个数字时,1111 1111是它所能表达最大的数。18的原码是0001 0010,99-18就类似于1111 1111-0001 0010=1110 1101,这个操作就是0变1,1变0求反码的操作,而结果正好是-18的反码(1110 1101),而后面的+1操作不就是补码等于反码+1的操作吗。
现在括号内的结果就类似于求-18的反码是:1110 1110,25的原码是0001 1001,我们试着相加一下:
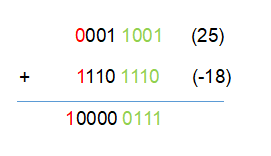
(补码方式相加)
结果是10000 0111,式子后面还有一个减去100(1 0000 0000)的操作,其实就是去掉二进制数的最高位,我们现在来看结果 0000 0111,反码的反码就是原码,因为它的最高是0,是正数,正数的原反补码都是一样的,0000 0111等于7,就是我们所求的答案。
再来一个例子 (-1)+(-3)

(补码方式相加)
结果11111 1100 我们去掉最高位 1111 1100,现在符号位是1为负数,这个数的反码是1000 0011,补码是1000 0100(补码的补码是原码),我们可以清楚的看到结果是-4,满足要求。
从上可以看出采用补码进行存储与运算,可以降低计算机的计算复杂度,提高计算效率。反码只是一个到达补码的桥梁,而存储原码会导致运算复杂度增大,效率低下。