所有的周期函数都可以用三角函数表示吗？

所有的周期函数都可以用三角函数表示吗？

https://www.zhihu.com/question/52396255

所有的周期函数都可以用三角函数表示吗？

呃，可能这个问题有点蠢，但是如果答案是否或者是都请给出证明，或者举一个反例然后证明其不能由三角函数表示出来（●─●）谢谢
呃，突然发现只要证明某个函数不能用三角函数表示就可以了，比如说反比例函数，取它的某一段作成周期函数，证明那一段不能用三角函数表示出来，可是还是不知道怎么证明，求助

数学话题下的优秀答主

1.先回答题主的问题：
函数可以展开成Fourier级数的充分必要条件我还没有见到过。现在可以用的一些命题是：
令 $[{s_n}left( {t,f} ight) = frac{1}{pi }int_{ - pi }^pi {fleft( x ight)} {D_n}left( {x - t} ight)dx]$ ，这是f的Fourier级数在一点t处的n阶部分和（它是个卷积哦），其中 $[{D_n}left( u ight) = frac{{sin left( {n + frac{1}{2}} ight)u}}{{2sin frac{1}{2}u}}]$ 为dirichlet核
那么lebesgue常数 $[{L_n} = {s_n}left( {0,{mathop{ m sgn}} {D_n}left( x ight)} ight) sim left( {frac{4}{{{pi ^2}}}} ight)ln nleft( {n o infty } ight)]$ 。这对于你判断一个三角级数是否是某函数(当然它要是 $L(E)$ 的)的Fourier系数会有帮助（必要条件）。
Fejer给出了一个充分条件：
假如函数是 $[Lleft( {left[ {0,2pi } ight]} ight)]$ 的，那么它的fourier级数在 $[{left[ {0,2pi } ight]}]$ 上几乎处处可切萨罗求和得这个函数。它的推论是：如果 $f$ 的fourier级数在正测度集 $E$ 上收敛，那么它在 $E$ 上几乎处处收敛于 $f$ 。

由是我们可以构造这样一个函数，使得一个 $[Lleft( {left[ {0,2pi } ight]} ight)]$ 的函数，它的fourier级数几乎处处无界发散：
在闭区间 $[{left[ {0,2pi } ight]}]$ 上选取n个点 $[{A_k} = frac{{4kpi }}{{left( {2n + 1} ight)}}]$ ，假定一列奇数满足： $[{lambda _1} = 1,k ge 2,{lambda _k} > n]$ ，定义一列数 $[left{ {{m_k}} ight}]$ 和一系列区间 $[left{ {{J_k}} ight}]$ 如下：
$[{m_k} + 1 = {lambda _k}left( {2n + 1} ight)]$ ， $[{J_k} = left[ {{A_k} - 1/{m_k}^2,{A_k} + 1/{m_k}^2} ight]]$ 。( $k=1,2,...n$ )
然后作函数： $[{varphi _n}left( x ight) = left{ egin{array}{l} {m_k}^2/n,x in {J_k} \ 0,x in left[ {0,2pi } ight]ackslash igcuplimits_{k = 1}^n {{J_k}} \ end{array} ight.]$ ，即为所需的反例。

这个周期函数就不可展成fourier级数。至于它的证明，实在太冗长了，也需要实变函数的知识才能理解。
傅里叶级数可以表示成某函数的充分必要条件很复杂（反正我还没见过），对它的研究主要还是集中在实变函数中。比较好的结果是在Dirichlet条件下的。
Dirichlet条件：设 $f$ 在 $[{left[ {0,2pi } ight]}]$ 上分段单调或分段可微（有可数个极值点），并且除可数多个第一类间断点外连续，则它的Fourier级数在 $[{left[ {0,2pi } ight]}]$ 上任一点 $x$ 收敛于 $[frac{{fleft( {{x_ + }} ight) + fleft( {{x_ - }} ight)}}{2}]$ 。

我想题主所需要的函数大多满足那样的条件。但一般的微积分教材中都有叙述，我就不再叙述了。
此外，fourier级数与幂级数不同。每一个给定的幂级数，都是某函数的taylor级数；但每一个给定的三角函数，却不一定是某函数的fourier级数。

2.如果给的函数性质足够好，我们如何构造这个三角函数的表示？
你只需要知道，在 $[{left[ {0,2pi } ight]}]$ 上， ${e_n(x)}$ = $left{ {frac{1}{{sqrt {2pi } }},...frac{{cos nx}}{{sqrt pi }},frac{{sin nx}}{{sqrt pi }}},.... ight}$ (n=1,2,...)中随便取两个乘起来再作积分，得到的是 ${delta _{ij}}$ （i=j时为1，i≠j时为0）。这样，我们先假定写成（ ${e_n(x)}$ 已知，但系数未知） $[f = sumlimits_{n = 1}^infty {{c_n}{e_n}left( x ight)} ]$ ，然后要算哪个 $c_n$ ，就两边同乘以 ${e_n(x)}$ ，积分就可以得到系数。

编辑于 2016-11-15

灵剑

数学话题下的优秀答主

当然并不是所有的，比如狄利克雷函数（所有有理数都是1，无理数都是0）。能用三角函数的级数表示的，比连续函数弱一点，至多可数个第一类间断点的周期函数可以用傅立叶级数表示。证明的话，学到就知道了。

编辑于 2016-11-15

@Say

说得很好了，Dirichlet条件对于一般的工程问题已经足够。
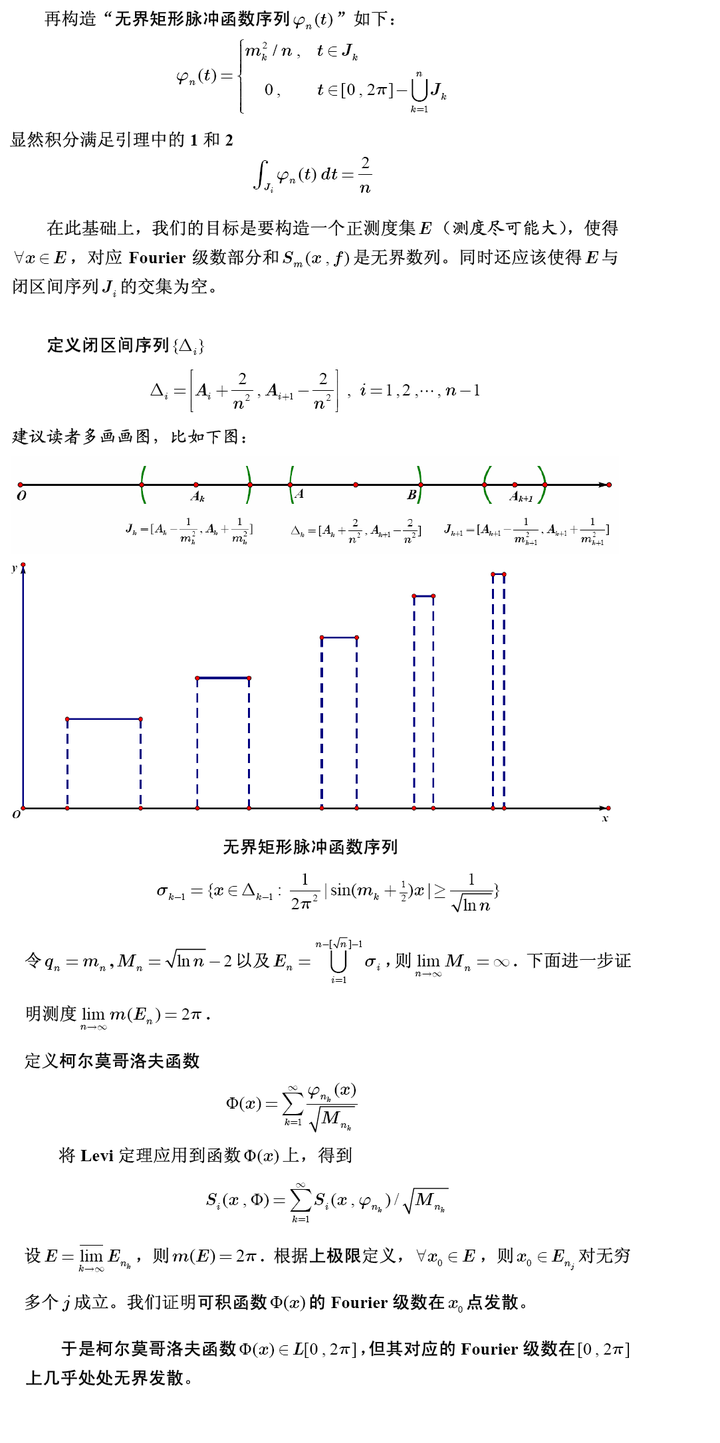
顺便补充一下反例的函数叫Колмогоров函数。

(以下资料来自：数学学习或研究中你见过哪些有意思的反例？ - 知乎用户的回答 - 知乎）

后来他把”几乎处处“加强到了”处处“，见他的这篇论文。

编辑于 2016-11-15

知乎

哪里有免费的云存储解决方案？

AWS提供全套免费云存储解决方案，为企业数字化转型助力! 6大免费套餐在云中部署存储和内容分发解决方案所需的免费产品和服务，让您的数据更安全。查看详情

知乎用户

这个问题很好。你可以去查一下一种叫傅立叶级数的东西。
结论是，如果这个函数性质不是很差，你可以把它表示为一列三角函数的和。

发布于 2016-11-09

再补充几个反例。摘自《实分析中的反例》汪林高等教育出版社 1989年10月第1版

即是上面Колмогоров函数。

发布于 2016-11-16

继续浏览内容

知乎

发现更大的世界

打开

Chrome

继续

夜行列车里的男爵

数学铸就三叉戟

不可以的三角函数只是一种特殊的周期函数而周期函数指的是函数在定义域内的一种现象
相关阅读:
Activiti(三)流程变量和流程实例
 vue(生命周期,钩子方法,组件)
Vue(指令篇)
Activiti(二)
使用MyBatis_Plus生成代码
 activiti
多线程常见面试题总结
 Dubbo集群-负载均衡
 dubbox入门
 事务的传播行为，隔离级别以及锁机制
原文地址：https://www.cnblogs.com/leoking01/p/14262899.html

所有的周期函数都可以用三角函数表示吗？

https://www.zhihu.com/question/52396255

所有的周期函数都可以用三角函数表示吗？

哪里有免费的云存储解决方案？