解决一个回溯问题,实际上就是一个决策树的遍历过程。你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
回溯算法的框架:核心
result = [] def backtrack(路径, 选择列表): if 满足结束条件: result.add(路径) return for 选择 in 选择列表: 做选择(选择剪枝判断) backtrack(路径, 选择列表) 撤销选择
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」。我们只要在递归之前做出选择,在递归之后撤销刚才的选择。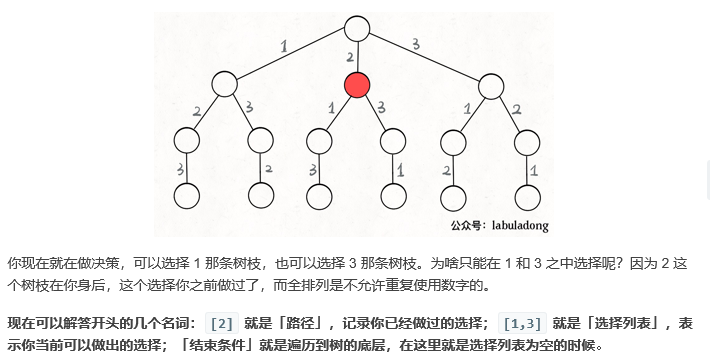
集合的全排列:
List<List<Integer>> res = new LinkedList<>(); /* 主函数,输入一组不重复的数字,返回它们的全排列 */ List<List<Integer>> permute(int[] nums) { // 记录「路径」 LinkedList<Integer> track = new LinkedList<>(); backtrack(nums, track); return res; } // 路径:记录在 track 中 // 选择列表:nums 中不存在于 track 的那些元素 // 结束条件:nums 中的元素全都在 track 中出现 void backtrack(int[] nums, LinkedList<Integer> track) { // 触发结束条件 if (track.size() == nums.length) { res.add(new LinkedList(track)); return; } for (int i = 0; i < nums.length; i++) { // 排除不合法的选择 if (track.contains(nums[i])) continue; // 做选择 track.add(nums[i]); // 进入下一层决策树 backtrack(nums, track); // 取消选择 track.removeLast(); } }

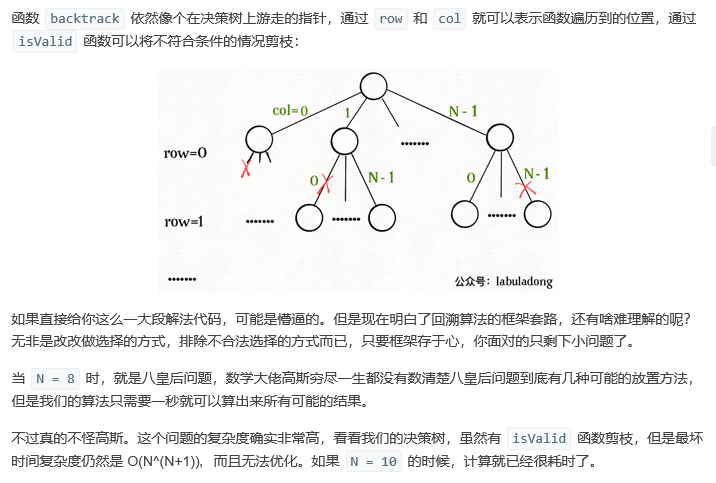
vector<vector<string>> res; /* 输入棋盘边长 n,返回所有合法的放置 */ vector<vector<string>> solveNQueens(int n) { // '.' 表示空,'Q' 表示皇后,初始化空棋盘。 vector<string> board(n, string(n, '.')); backtrack(board, 0); return res; } // 路径:board 中小于 row 的那些行都已经成功放置了皇后 // 选择列表:第 row 行的所有列都是放置皇后的选择 // 结束条件:row 超过 board 的最后一行 void backtrack(vector<string>& board, int row) { // 触发结束条件 if (row == board.size()) { res.push_back(board); return; } int n = board[row].size(); for (int col = 0; col < n; col++) { // 排除不合法选择 if (!isValid(board, row, col)) continue; // 做选择 board[row][col] = 'Q'; // 进入下一行决策 backtrack(board, row + 1); // 撤销选择 board[row][col] = '.'; } }
/* 是否可以在 board[row][col] 放置皇后? */ bool isValid(vector<string>& board, int row, int col) { int n = board.size(); // 检查列是否有皇后互相冲突 for (int i = 0; i < n; i++) { if (board[i][col] == 'Q') return false; } // 检查右上方是否有皇后互相冲突 for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) { if (board[i][j] == 'Q') return false; } // 检查左上方是否有皇后互相冲突 for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) { if (board[i][j] == 'Q') return false; } return true; }
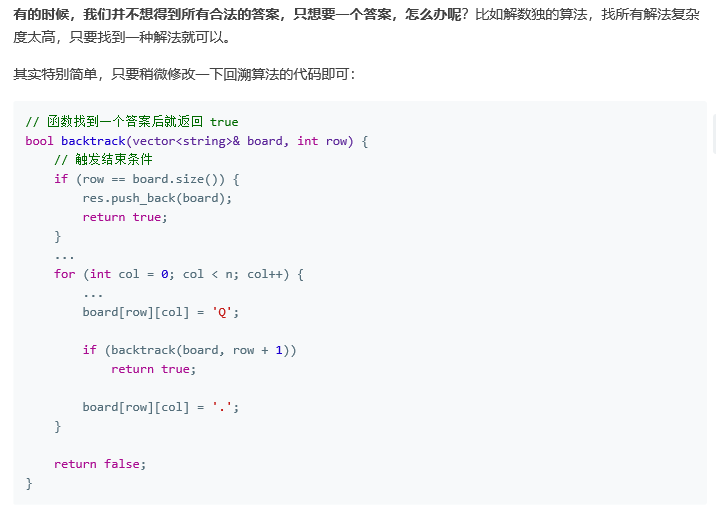

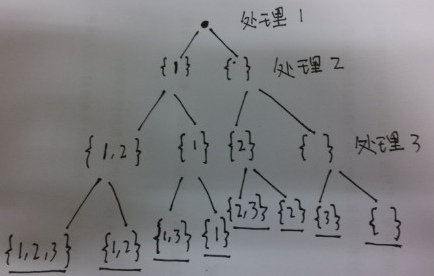
class Solution { public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> res=new ArrayList<>(); res.add(new ArrayList()); for(int emp: nums) { for(int i=res.size()-1;i>=0;i--) { ArrayList list=new ArrayList(res.get(i)); list.add(emp); res.add(list); } } return res; } }
class Solution { public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> res=new ArrayList<>(); backtrack(nums,res,new ArrayList<Integer>(),0); return res; } public void backtrack(int [] nums,List<List<Integer>> res,ArrayList<Integer> list, int start ) { res.add(new ArrayList(list)); for(int i=start;i<nums.length;i++) { list.add(nums[i]); backtrack(nums,res,list,i+1); list.remove(list.size()-1); } } }

import java.util.ArrayList; /** public class TreeNode { int val = 0; TreeNode left = null; TreeNode right = null; public TreeNode(int val) { this.val = val; } } */ public class Solution { ArrayList<ArrayList<Integer>> list =new ArrayList<>(); public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) { ArrayList<Integer> res=new ArrayList<>(); if(root==null || target<0) return list; findPath(root,res,target); return list; } public void findPath(TreeNode root,ArrayList<Integer> res,int target){ if(root==null) return; res.add(root.val); int num=0; for(int i=0;i<res.size();i++) { num+=res.get(i); } if(target==num && root.left==null && root.right==null){ list.add(new ArrayList<Integer>(res)); } findPath(root.left,res,target); findPath(root.right,res,target); res.remove(res.size()-1); } }
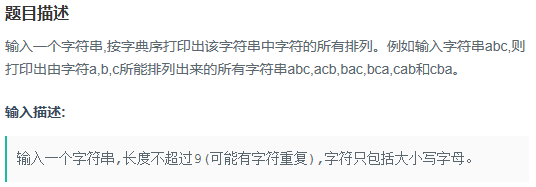
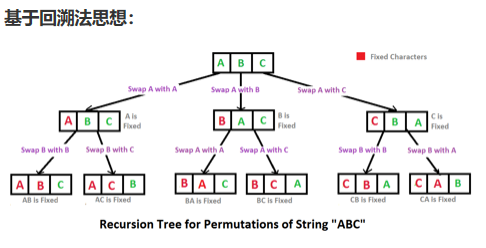
//有重复字母的全排列
import java.util.*; public class Solution { ArrayList<String> list=new ArrayList<String>(); public ArrayList<String> Permutation(String str) { if(str==null || str.length()==0) return list; help(str.toCharArray(),0); Collections.sort(list); return list; } public void help(char[] str, int i){ if(str.length-1==i){ String s=String.valueOf(str); if(!list.contains(s)){ list.add(s); } return; } for(int j=i;j<str.length;j++){ swap(str,i,j); help(str,i+1); swap(str,i,j); } } public void swap(char [] str,int i,int j){ char temp=str[i]; str[i]=str[j]; str[j]=temp; } }