2018 蓝桥杯省赛 B 组模拟赛(一)
A、今天蒜头君带着花椰妹和朋友们一起聚会,当朋友们问起年龄的时候,蒜头君打了一个哑谜(毕竟年龄是女孩子的隐私)说:“我的年龄是花椰妹年龄个位数和十位数之和的二倍”。
花椰妹看大家一脸懵逼,就知道大家也不知道蒜头君的年龄,便连忙补充道:“我的年龄是蒜头君个位数和十位数之和的三倍”。
请你计算:蒜头君和花椰妹年龄一共有多少种可能情况?
提醒:两位的年龄都是在 [10,100)[10,100) 这个区间内。
题解: 暴力枚举
answer: 1
代码如下:

#include <iostream> #include <cstdio> using namespace std; int main() { int ans=0; for(int i=10;i<100;i++) { int x=2*(i%10+i/10); if(10<=x&&x<100&&i==3*(x%10+x/10)) ans++; } printf("%d ",ans); return 0; }
B、蒜头君今天回到了老家的大宅院,老家的灯还是那中拉线的灯(拉一次为亮,再拉一次就灭),蒜头君觉得无聊。把 10001000 盏灯 3的倍数拉了一次,5的倍数拉了一次,7的倍数拉了一次(灯得的编号从 1-10001−1000,灯的初始状态都是亮的)。这个时候蒜头君在想还剩下几盏灯还在亮着?
提示:请不要输出多余的符号。
题解:还是暴力,可以初始化一个数组全为0(表示灯全亮),然后跑三个for循环,第一次循环,若是3的倍数,该元素的值就去反,同理,第二次,5的倍数,第三次7的倍数
answer: 571
代码如下:

#include <iostream> #include <cstdio> #include <cstring> using namespace std; const int N=1e3+7; int vis[N]={0}; int main() { int ans=0; for(int i=1;i<=1000;i++) if(!(i%3)) vis[i]=!vis[i]; for(int i=1;i<=1000;i++) if(!(i%5)) vis[i]=!vis[i]; for(int i=1;i<=1000;i++) if(!(i%7)) vis[i]=!vis[i]; for(int i=1;i<=1000;i++) if(!vis[i]) ans++; printf("%d ",ans); return 0; }
C、最近蒜头君喜欢上了U型数字,所谓U型数字,就是这个数字的每一位先严格单调递减,后严格单调递增。比如 212212 就是一个U型数字,但是 333333, 9898, 567567, 3131331313,就是不是U型数字。
现在蒜头君问你,[1,100000][1,100000] 有多少U型数字?
提示:请不要输出多余的符号。
题解:可以先找到最小值的位置,若最小值的位置在两头,不是U行数字,让后判断两断是否严格递减和递增
answer: 8193
代码如下:

def path(x,index): if index==0 or index==len(x)-1: return False else: for i in range(index): if x[i]<=x[i+1]: return False for i in range(index,len(x)-1): if x[i]>=x[i+1]: return False return True if __name__ == '__main__': ans=0 for i in range(100,100001): x=str(i) minn=x[0] index=0 for j in range(len(x)): if minn>=x[j]: minn=x[j] index=j if path(x,index): ans=ans+1 print(ans)
D、LIS是最长上升子序列。什么是最长上升子序列? 就是给你一个序列,请你在其中求出一段最长严格上升的部分,它不一定要连续。
就像这样:22, 33, 44, 77 和 22, 33, 44, 66 就是序列 22 55 3344 11 77 66 的两个上升子序列,最长的长度是 44。
题解:典型的dp题,f[i]表示前i个数字的上升子序列的最长长度,状态方程为: f[i]=max(f[i],f[j]+1);
代码如下:

#include<stdio.h> #include<stdlib.h> #include<string.h> int f[10000], b[10000]; int max(int a, int b) { return a > b ? a : b; } int lis(int n) { memset(f, 0, sizeof f); int res = 0; for (int i = 0; i < n; ++i) { for (int j = 0; j < i; ++j) { if (b[j] < b[i]) { f[i]=max(f[i],f[j]+1); } } res = max(res, f[i]); } return res+1; } int main() { int n; scanf("%d", &n); for (int i = 0; i < n; ++i) { scanf("%d", b + i); } printf("%d ", lis(n)); return 0; }
E、相信大家都知道什么是全排列,但是今天的全排列比你想象中的难一点。我们要找的是全排列中,排列结果互不相同的个数。比如:aab 的全排列就只有三种,那就是aab,baa,aba。
代码框中的代码是一种实现,请分析并填写缺失的代码。
该全排列用的是dfs , 代码片段要填的主要功能是:去重,因此当str[i]==str[j]&&vis[j]成立 ,跳出
代码如下:

#include <stdio.h> #include <stdlib.h> #include <string.h> #define N 1000 char str[N], buf[N]; int vis[N], total, len; void arrange(int num) { int i, j; if (num == len) { printf("%s ", buf); total++; return; } for (i = 0; i < len; ++i) { if (!vis[i]) { for (j = i + 1; j < len; ++j) { if (str[i]==str[j]&&vis[j]) { break; } } if (j == len) { vis[i] = 1; buf[num] = str[i]; arrange(num + 1); vis[i] = 0; } } } } int main() { while (~scanf("%s", str)) { len = strlen(str); int i, j; for (i = 0; i < len; ++i) { for (j = i + 1; j < len; ++j) { if (str[i] > str[j]) { char tmp = str[i]; str[i] = str[j]; str[j] = tmp; } } } total = 0; buf[len] = '�'; arrange(0); printf("Total %d ", total); } return 0; }
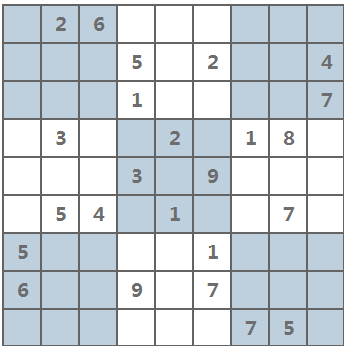
F、蒜头君今天突然开始还念童年了,想回忆回忆童年。他记得自己小时候,有一个很火的游戏叫做数独。便开始来了一局紧张而又刺激的高阶数独。蒜头君做完发现没有正解,不知道对不对? 不知道聪明的你能否给出一个标准答案?
标准数独是由一个给与了提示数字的 9×9 网格组成,我们只需将其空格填上数字,使得每一行,每一列以及每一个 3×3 宫都没有重复的数字出现。
输出这个数独得正解,输出格式如下:
* 2 6 * * * * * *
* * * 5 * 2 * * 4
* * * 1 * * * * 7
* 3 * * 2 * 1 8 *
* * * 3 * 9 * * *
* 5 4 * 1 * * 7 *
5 * * * * 1 * * *
6 * * 9 * 7 * * *
* * * * * * 7 5 *
把上面的 * 替换成 1 - 9就可以了
提醒:两个数字之间要有一个空格,其他地方不要输出多余的符号。
题解:两种做法,一种 是人工计算
另一种,则是dfs 得到一种就要停止
代码如下:

#include<bits/stdc++.h> using namespace std; int mmap[9][9]={ 0,2,6,0,0,0,0,0,0, 0,0,0,5,0,2,0,0,4, 0,0,0,1,0,0,0,0,7, 0,3,0,0,2,0,1,8,0, 0,0,0,3,0,9,0,0,0, 0,5,4,0,1,0,0,7,0, 5,0,0,0,0,1,0,0,0, 6,0,0,9,0,7,0,0,0, 0,0,0,0,0,0,7,5,0}; int flag=0,vis[9][9]; vector<pair<int,int> >v; void dfs(int num) { if(num>=v.size()||flag) { flag=1; return; } int x=v[num].first,y=v[num].second; for(int i=1;i<=9;i++) { if(flag) return; int flag1=0; for(int j=0;!flag1&&j<9;j++) if(mmap[x][j]==i&&vis[x][j]) { flag1=1; break; } for(int j=0;!flag1&&j<9;j++) if(mmap[j][y]==i&&vis[j][y]) { flag1=1; break; } int fx=(x/3)*3,fy=(y/3)*3; for(int ix=fx;!flag1&&ix<fx+3;ix++) for(int jy=fy;!flag1&&jy<fy+3;jy++) if(mmap[ix][jy]==i&&vis[ix][jy]) { flag1=1; break; } if(!flag1) { vis[x][y]=1; mmap[x][y]=i; dfs(num+1); vis[x][y]=0; } } } int main() { v.clear(); memset(vis,0,sizeof(vis)); for(int i=0;i<9;i++) for(int j=0;j<9;j++) if(!mmap[i][j]) v.push_back(make_pair(i,j)); else vis[i][j]=1; cout<<v.size()<<endl; dfs(0); for(int i=0;i<9;i++) { for(int j=0;j<9;j++) printf("%d%c",mmap[i][j],j==8?' ':' '); } return 0; } /* * 2 6 * * * * * * * * * 5 * 2 * * 4 * * * 1 * * * * 7 * 3 * * 2 * 1 8 * * * * 3 * 9 * * * * 5 4 * 1 * * 7 * 5 * * * * 1 * * * 6 * * 9 * 7 * * * * * * * * * 7 5 * */
G、
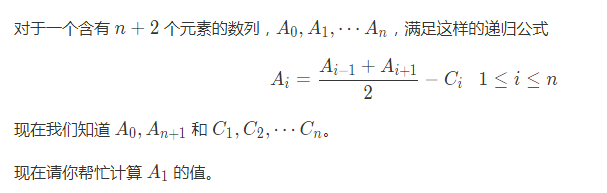
代码如下:

#include <bits/stdc++.h> using namespace std; const int N=1e3+7; int main() { double a[N],c[N],ed; int n; scanf("%d",&n); scanf("%lf%lf",&a[0],&ed); a[1]=0; for(int i=1;i<=n;i++) { scanf("%lf",&c[i]); a[i+1]=2*a[i]+2*c[i]-a[i-1]; } printf("%.2lf ",(ed-a[n+1])/(n+1)); return 0; }
H、蒜头君被暗黑军团包围在一座岛上,所有通往近卫军团的路都有暗黑军团把手。幸运的是,小岛上有一扇上古之神打造的封印之门,可以通往近卫军团,传闻至今没有人能解除封印。
封印之门上有一串文字,只包含小写字母,有 kk种操作规则,每个规则可以把一个字符变换成另外一个字符。经过任意多次操作以后,最后如果能把封印之门上的文字变换成解开封印之门的文字,封印之门将会开启。
蒜头君战斗力超强,但是不擅计算,请你帮忙蒜头君计算至少需要操作多少次才能解开封印之门。
输入格式
输入第一行一个字符串,长度不大于 10001000,只包含小写字母,表示封印之门上的文字。
输入第二行一个字符串,只包含小写字母,保证长度和第一个字符串相等,表示能解开封印之门的文字。
输入第三行一个整数 k(0 le k le 676)k(0≤k≤676)。
接下来 kk 行,每行输出两个空格隔开的字符 aa, bb,表示一次操作能把字符 aa 变换成字符 bb。
输出格式
如果蒜头君能开启封印之门,输出最少的操作次数。否则输出一行 -1−1。
样例输入
abcd dddd 3 a b b c c d
样例输出
6
题解: floyd 最短路
代码如下:

#include <bits/stdc++.h> using namespace std; const int N=28; const int M=1e3+7; const int inf=(1<<30)-1; int dis[N][N]; void floyd() { for(int k=1;k<27;k++) for(int i=1;i<27;i++) for(int j=1;j<27;j++) if(dis[i][j]>=dis[i][k]+dis[k][j]) dis[i][j]=dis[i][k]+dis[k][j]; } int main() { char st[M],ed[M]; scanf("%s",st); scanf("%s",ed); int len=strlen(st); int m,ans=0; scanf("%d",&m); for(int i=1;i<28;i++) { for(int j=1;j<28;j++) dis[i][j]=inf; dis[i][i]=0; } while(m--) { char s[3],e[3]; scanf("%s%s",s,e); if(s[0]!=e[0]) dis[s[0]-'a'+1][e[0]-'a'+1]=1; } floyd(); for(int i=0;i<len;i++) { if(dis[st[i]-'a'+1][ed[i]-'a'+1]>=inf) { puts("-1"); return 0; } ans+=dis[st[i]-'a'+1][ed[i]-'a'+1]; } printf("%d ",ans); return 0; }
I、在一个星光摧残的夜晚,蒜头君一颗一颗的数这天上的星星。
蒜头君给在天上巧妙的画了一个直角坐标系,让所有的星星都分布在第一象。天上有 n 颗星星,他能知道每一颗星星的坐标和亮度。
现在,蒜头君问自己 q 次,每次他问自己每个矩形区域的星星的亮度和是多少(包含边界上的星星)。
输入格式
第一行输入一个整数 n(1≤n≤50000) 表示星星的数量。
接下里 nn 行,每行输入三个整数 x,y,w(0≤x,y,w≤2000),表示在坐标 (x,y) 有一颗亮度为 w 的星星。注意一个点可能有多个星星。
接下来一行输入一个整数 q(1≤q≤50000),表示查询的次数。
接下来 qq 行,每行输入四个整数 x1,y1,x2,y2,其中 (x1,y1) 表示查询的矩形的左下角的坐标,(x2,y2) 表示查询的矩形的右上角的坐标,0≤x1≤x2≤2000,0≤y1≤y2≤2000。
输出格式
对于每一次查询,输出一行一个整数,表示查询的矩形区域内的星星的亮度总和。
样例输入
5 5 0 6 7 9 7 8 6 13 9 7 1 3 0 19 4 0 8 7 9 0 0 7 10 2 7 10 9 5 4 7 5
样例输出
7 32 8 0
题解:维护前缀和 和 容斥原理
代码如下:

#include <bits/stdc++.h> using namespace std; const int N=2*1e3+7; int sum[N][N],mmap[N][N]; int main() { int n,q; memset(sum,0,sizeof(sum)); memset(mmap,0,sizeof(mmap)); scanf("%d",&n); while(n--) { int x,y,w; scanf("%d%d%d",&x,&y,&w); mmap[x+1][y+1]+=w; } for(int i=1;i<N;i++) for(int j=1;j<N;j++) sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+mmap[i][j]; scanf("%d",&q); while(q--) { int stx,sty,edx,edy; scanf("%d%d%d%d",&stx,&sty,&edx,&edy); printf("%d ",sum[edx+1][edy+1]-(sum[edx+1][sty]+sum[stx][edy+1]-sum[stx][sty])); } return 0; }
J、
武当派一共有 n 人,门派内 n 人按照武功高低进行排名,武功最高的人排名第 1,次高的人排名第 2,... 武功最低的人排名第 n。现在我们用武功的排名来给每个人标号,除了祖师爷,每个人都有一个师父,每个人可能有多个徒弟。
我们知道,武当派人才辈出,连祖师爷的武功都只能排行到 p。也就是说徒弟的武功是可能超过师父的,所谓的青出于蓝胜于蓝。
请你帮忙计算每个人的所有子弟(包括徒弟的徒弟,徒弟的徒弟的徒弟....)中,有多少人的武功超过了他自己。
输入格式
输入第一行两个整数 n,p(1≤n≤100000,1≤p≤n)。
接下来 n−1 行,每行输入两个整数 u,v(1≤u,v≤n),表示 u 和 v 之间存在师徒关系。
输出格式
输出一行 n 个整数,第 i 个整数表示武功排行为 i 的人的子弟有多少人超过了他。
行末不要输出多余的空格。
样例输入
10 5 5 3 5 8 3 4 3 1 2 1 6 7 8 7 9 8 8 10
样例输出
0 0 2 0 4 0 1 2 0 0
题解:将数dfs序列化,然后用树状数组维护
代码如下:

#include <bits/stdc++.h> using namespace std; const int N=1e5+7; vector<int>edge[N]; int t,in[N],out[N],c[N]; int lowbit(int x) { return x&(-x); } int updata(int x,int y) { int i=x; while(i<=t) { c[i]+=y; i+=lowbit(i); } } int query(int x) { int ans=0; while(x) { ans+=c[x]; x-=lowbit(x); } return ans; } void dfs(int u,int pre) { in[u]=++t; int len=edge[u].size(); for(int i=0;i<len;i++) { int v=edge[u][i]; if(v!=pre) dfs(v,u); } out[u]=t; } int main() { int n,p,u,v; scanf("%d%d",&n,&p); memset(c,0,sizeof(c)); for(int i=1;i<n;i++) { scanf("%d%d",&u,&v); edge[u].push_back(v); edge[v].push_back(u); } t=0; dfs(p,0); for(int i=1;i<=n;i++) { printf("%d%c",query(out[i])-query(in[i]),i==n?' ':' '); updata(in[i],1); } return 0; }