向量是同时具有 大小 、方向 的物理量。
向量一般可以用来表示:
- 力 :朝一个方向上作用一定大小的力量
- 位移:朝一个方向移动一定距离
- 速度:朝一个方向单位时间移动一定距离
- 方向:朝某一个方向。
向量特性:
- 只能平移
- 无法旋转
- 无法缩放
向量的数学运算:
- 向量 X 标量:表示将该向量的长度放大 N倍。向量A = (x,y,z);标量N,则 N*A = (nx,ny,nz);
- 向量相加:
几何意如下图,
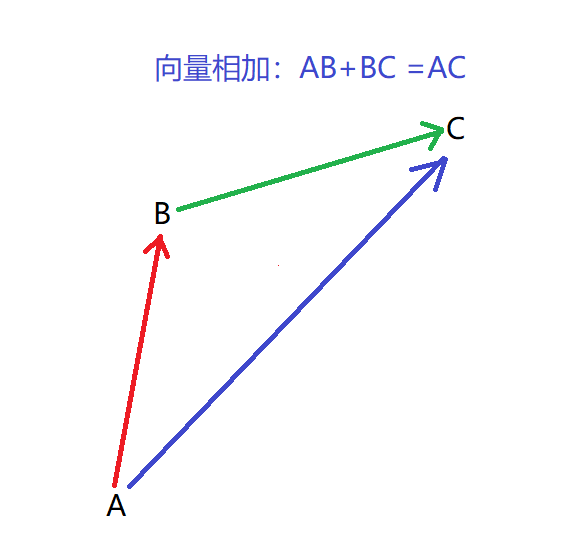
数学算数:AB =(x,y,z) BC=(a,b,c), AB+BC =(x+a,y+b,z+c)
- 向量相减:
几何意义如下图,(共起点,连终点,方向指向 被减向量)
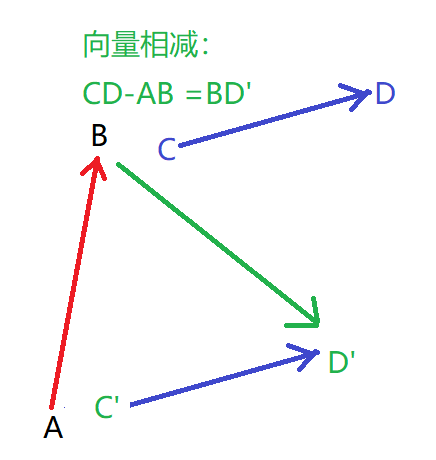
数学算法:AB =(x,y,z) CD=(a,b,c), CD-AB=(a-x,b-y,c-z)
向量叉乘:2D向量没有叉乘运算,只有3D向量有,3D向量的叉乘运算得到的结果仍是一个3D向量:
几何意义如下图
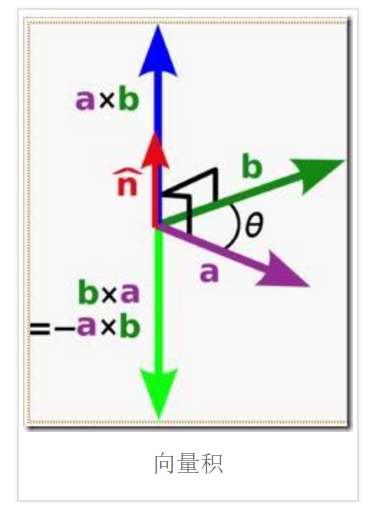
|c| =|a|*|b|*sin<a,b>,表示两个向量叉乘,得到的结果向量c 的模长 = 向量a 与向量b组成的平行四边形的面积
c的方向,则根据向量所处的坐标系是左手坐标系还是右手坐标系来确定方向。
向量叉乘的数学公式为: a=(x,y,z) ,b = (α,β,δ),则c = a x b = (y*δ-z*β,z*α-x*δ,x*β-y*α)
看公式就已经知道,向量的叉乘是不满足交换律的,及 a X b != b X a;
向量点乘:向量点乘得到的是一个标量,计算公式为:
标量c = |a|*|b|*cos<a,b>(两个向量的模乘以两个向量夹角的余弦值)。
a=(x,y,z) ,b = (α,β,δ),则c = a•b =x*α+y*β+z*δ