简单相关性分析(两个连续型变量)

转自：https://zhuanlan.zhihu.com/p/36441826

目录：

• 变量间的关系分析
• 函数关系
• 相关关系
• 平行关系
• 依存关系
• 简单相关分析
• 计算两变量之间的线性相关系数
• 协方差定义、柯西-施瓦尔兹不等式
• Pearson 相关系数
• 相关系数的假设检验
• 的图
• t-检验的解读
• 纯探讨向——深度探讨

一、变量间的关系分析

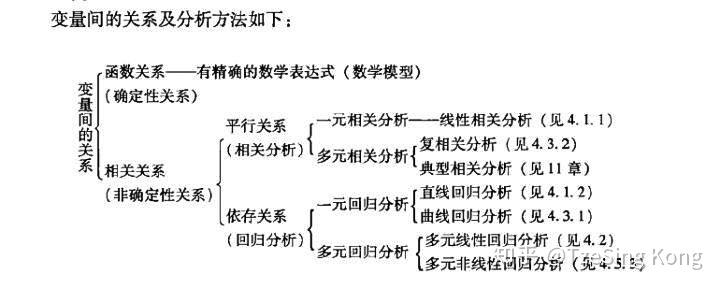
变量之间的关系可分为两类：

1. 存在完全确定的关系——称为函数关系
2. 不存在完全确定的关系——虽然变量间有着十分密切的关系，但是不能由一个或多各变量值精确地求出另一个变量的值，称为相关关系，存在相关关系的变量称为相关变量

相关变量的关系也可分为两种：

1. 两个及以上变量间相互影响——平行关系
2. 一个变量变化受另一个变量的影响——依存关系

它们对应的分析方法：

• 相关分析是研究呈平行关系的相关变量之间的关系
• 回归分析是研究呈依存关系的相关变量之间的关系

回归分析和相关分析都是研究变量之间关系的统计学课题，两种分析方法相互结合和渗透

---

二、简单相关分析

相关分析：就是通过对大量数字资料的观察，消除偶然因素的影响，探求现象之间相关关系的密切程度和表现形式

主要研究内容：现象之间是否相关、相关的方向、密切程度等，不区分自变量与因变量，也不关心各变量的构成形式

主要分析方法：绘制相关图、计算相关系数、检验相关系数

1、计算两变量之间的线性相关系数

所有相关分析中最简单的就是两个变量间的线性相关，一变量数值发生变动，另一变量数值会随之发生大致均等的变动，各点的分布在平面图上大概表现为一直线。

二元总体X与Y散点图

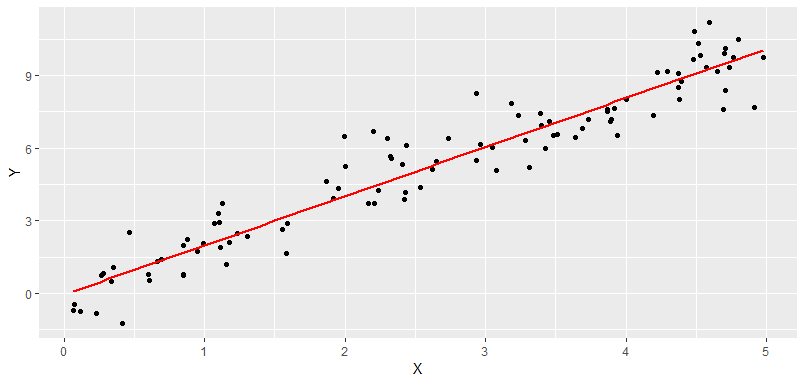
线性相关分析，就是用线性相关系数来衡量两变量的相关关系和密切程度

给定二元总体

总体相关系数用 来表示：

为 的总体方差，

是 的总体方差，

是 与 的协方差。

浅谈一下协方差定义：

设 是二维随机变量，若 存在，

则称 ，叫 与 的协方差，也叫 与 的相关（中心）矩

即 的偏差" "与 的偏差" "乘积的期望。

解读：

• 当 ， 的偏差" "跟 的偏差" "，有同时增加或同时减少的倾向，又由于 和 都是常数，所以就能够等价于 与 有同时增加或者减少的倾向，称 与 正相关
• 当 ， 的偏差" "跟 的偏差" "，有 增加 减少的倾向，或 增加 减少的倾向，称 与 负相关
• 当 ，称 与 不相关，这时可能是“ 与 取值毫无关联”，也可能是“有某种特殊的非线性关系”

根据柯西-施瓦尔兹不等式(Cauchy–Schwarz inequality)：

变形得 在区间

是没有单位的，因为分子协方差的量纲除以了分母的与分子相同的量纲

• 两变量线性相关性越密切， 接近于
• 两变量线性相关性越低， 接近于
• 的情况跟上面 情况一样

协方差与相关系数的关系，就像绝对数与相对数的关系。

Pearson 相关系数(样本线性相关系数)

但是，学过统计的都知道，我们一般用样本线性相关系数来估计总体线性相关系数

设 是二元总体，简单随机抽样 ，，......，

样本均值： ，

样本方差： ，

样本协方差：

样本相关系数：

为 的离差平方和， 为 的离差平方和， 为 与 离差乘积之和(可正可负)

实际计算可按下面简化：

例子：研究身高与体重的关系(R语言)

> x <- c(171,175,159,155,152,158,154,164,168,166,159,164)
> y <- c(57,64,41,38,35,44,41,51,57,49,47,46)
> plot(x,y)
> lxy <- function(x,y){
+     n = length(x);
+     return(sum(x*y)-sum(x)*sum(y)/n)
+ }
> lxy(x,x)
[1] 556.9167
> lxy(y,y)
[1] 813
> lxy(x,y)
[1] 645.5
> r <- lxy(x,y)/sqrt(lxy(x,x)*lxy(y,y))
> r
[1] 0.9593031
也能直接用cor()
> cor(x,y)

[1] 0.9593031

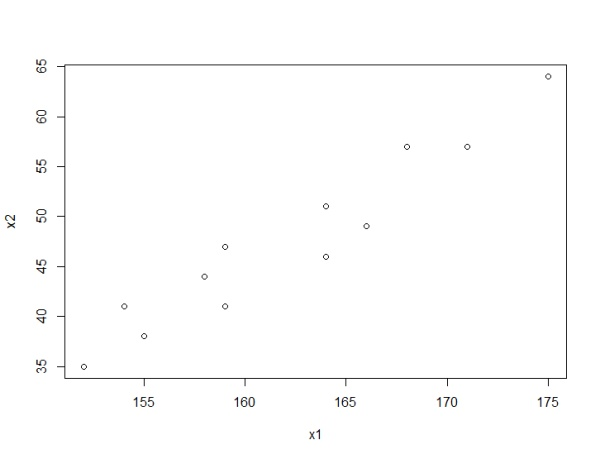
这里的 ，说明身高和体重是正的线性相关关系

至于 是否显著，就要看下面的显著性检验了。

Python版本的代码如下：

>>> import numpy as np

>>> import matplotlib.pyplot as plt

>>> x = np.array([171,175,159,155,152,158,154,164,168,166,159,164])

>>> y = np.array([57,64,41,38,35,44,41,51,57,49,47,46])

>>> np.corrcoef(x, y)

array([[1.        , 0.95930314],

[0.95930314, 1.        ]])

>>> plt.scatter(x, y)

>>> plt.show()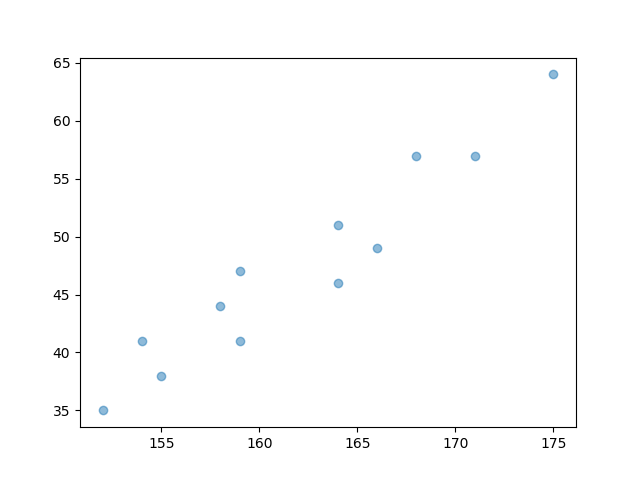

---

2、相关系数的假设检验

引入假设检验的原因： 与其他统计指标一样，也会有抽样误差。从同一总体内抽取若干大小相同的样本，各样本的样本相关系数总会有波动。即根据样本数据是否有足够的证据得出总体相关系数不为0的结论

要判断不等于 的 值是来自总体相关系数 的总体，还是来自 的总体，必须进行显著性检验

由于来自 的总体的所有样本相关系数呈白噪声或者其他特殊分布

（为什么？看图第一行中间、第三行）

因为样本间没有线性相关性，可能会杂乱无章(即什么关系也没有)，也可能呈现出一些非线性关系(更高阶的关系Pearson相关系数并不能表示出来)

图片来自Wiki

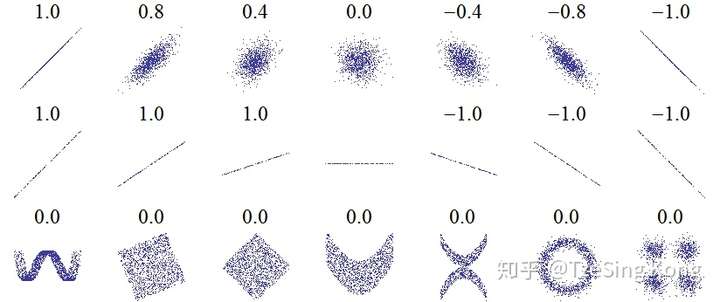
关于 会在第 3 章继续探讨

所以 的显著性检验可以用双侧 检验来进行

（1）建立检验假设：

（2）构造 统计量，计算相关系数 的 值：

此 近似服从 分布，如果数据严格服从二元正态分布

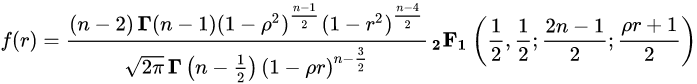
是 gamma 函数， 是高斯超几何函数。

当总体相关系数 时（假定两个随机变量是正态无相关的），样本相关系数 的密度函数为： ， 是 beta 函数，此密度函数碰巧就是统计量 就是自由度为 的 分布；

（3）计算 值和 值，做结论

在 R语言 中有 cor.test() 函数

# r的显著性检验,参数alternative默认是"two.side"即双侧t检验

method默认"pearson"
> cor.test(x1, x2)
Pearson's product-moment correlation

data:  x1 and x2

t = 10.743, df = 10, p-value = 8.21e-07

alternative hypothesis: true correlation is not equal to 0

95 percent confidence interval:

0.8574875 0.9888163

sample estimates:

cor

0.9593031

R的 cor.test() 在这里给出的结果还是比较丰富的。

• 值为
• 自由度是
• ，在显著性水平 上拒绝 ，接受 认为该人群身高和体重成正线性关系
• 置信度为 的区间估计是 ，意思是总体线性相关系数 取值在 上的概率是
• 的点估计为

这段检验该如何解读？

这段代码检验了身高和体重的Pearson相关系数为 的原假设

假设总体相关度为 ，则预计在一百万次中只会有少于一次的机会见到 这样大的相关度（即 ）

但其实这种情况几乎不可能发生，所以可以拒绝掉原假设，即身高和体重的总体相关度不为

注意：

相关系数的显著性是与自由度 有关，也就是与样本数量 有关（这也是相关系数很明显的缺点）。

样本量小，相关系数绝对值容易接近于 ，样本量大，相关系数绝对值容易偏小。

容易给人一种假象

在样本量很小 ，自由度 时，虽然 却是不显著

在样本量很大 时，即使 ，也是显著的

所以不能只看 值就下结论，还要看样本量大小

所以，我们要拿到充分大的样本，就能把样本相关系数 作为总体相关系数 ，这样就不必关心显著性检验的结果了

---

3、 与无法度量非线性关系的强度

举《Statisitcal Inference第二版》里面的例子4.5.9

，

令 ，其中 ， 与 独立即

但是

进而

但明明是类似于二阶抛物线的关系，Pearson相关系数却为 ？！！

这就明显说明了Pearson相关系数无法度量非线性关系的强度

---

下次会继续深入探讨多变量相关性分析

江子星：多变量相关性分析(一个因变量与多个自变量)​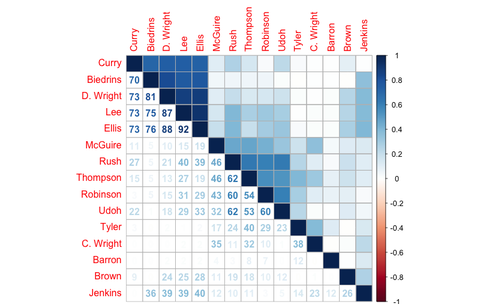zhuanlan.zhihu.com

参考书籍：

• 《多元统计分析及R语言》第四版——王斌会
• 《概率论与数理统计教程》第二版——茆诗松 / 程依鸣 / 濮晓龙
• 《R语言实战》第2版——Robert I. Kabacoff
• 《Statistical Inference》——George Casella / Roger L. Berger
• 相关系数检验 Using the exact distribution https://en.wikipedia.org/wiki/Pearson_correlation_coefficient