排序算法

1.冒泡排序(Bubble Sort)

最简单的排序方法是冒泡排序方法,这种方法的基本思想是,将待排序的元素看作是竖着排列的"气泡",较小的元素比较轻,从而要往上浮,在冒泡排序算法中我们要对这个"气泡"序列处理若干遍,所谓一遍处理,就是自低向上检查一遍这个序列,并时刻注意两个相邻的元素的顺序是否正确,如果发现两个相邻元素的顺序不对,即"轻"的元素在下面,就交换它们的位置,显然,处理一遍之后,"最轻"的元素就浮到了最高的位置,处理二遍之后,"次轻"的元素就浮到了次高的位置,在作第二遍处理时,由于最高位置上的元素已是"最轻"元素.所以不必检查,一般地,第n便处理时,不必检查第n高位置以上的元素,因为经过前面n-1遍的处理,它们已正确地排好序;

/**
     *冒泡排序
     */
    void doBubbleSort(int[] src)
    {
       int len=src.length;
       for(int i=0;i<len;i++)
       {
           for(int j=i+1;j<len;j++)
           {
              int temp;
              if(src[i]>src[j])
              {
                  temp=src[j];
                  src[j]=src[i];
                  src[i]=temp;
              }            
           }
           printResult(i,src);
       }     
    }

2.选择排序(Selection Sort)

选择排序的基本思想是:对待排序的记录序列进行n-1遍处理,第一遍处理是将L[1....n]中最小者与L[1]交换位置,第2遍处理是将L[2...n]中最小者与L[2]交换位置,,,,第i遍处理是将L[i...n]中最小者与L[i]交换位置,这样经过i遍处理之后,前i个记录的位置就已经按从小到大的顺序排列好了.

当然,在实际操作时,也可以根据需要,通过从待排序的记录中选择最大者与其首记录交换位置,按从大到小的顺序进行排序处理.

/**
     *选择排序
     */
    void doChooseSort(int[] src)
    {
       int len=src.length;
       int temp;
       for(int i=0;i<len;i++)
       {
           temp=src[i];
           int j;
           int samllestLocation=i;//最小数的下标
           for(j=i+1;j<len;j++)
           {
              if(src[j]<temp)
              {
                  temp=src[j];//取出最小值
                  samllestLocation=j;//取出最小值所在下标
              }
           }
           src[samllestLocation]=src[i];
           src[i]=temp;
           printResult(i,src);
       }
    }

3.插入排序(Insertion Sort)

插入排序的基本思想是,经过i-1遍处理后,L[1...i-1]已排好序列,第i遍处理仅将L[i]插入L[1...i-1]的适当位置,使得L[1...i]又是排好序的序列,要达到这个目的,我们可以用顺序比较的方法

插入排序就是每一步都将一个待排数据按其大小插入到已经排序的数据中的适当位置,知道全部插入完毕,插入排序方法分直接插入排序和折半插入排序两种.

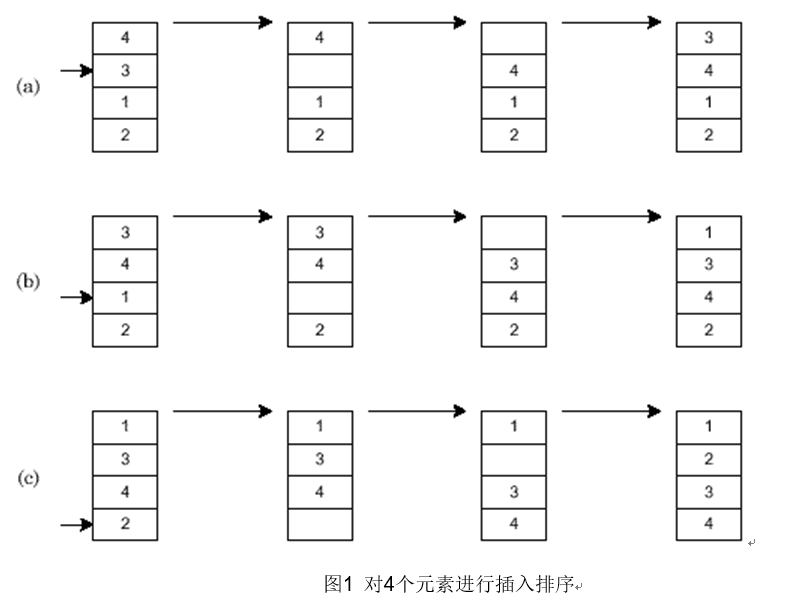
图1演示了对4个元素进行直接插入排序的过程，共需要(a),(b),(c)三次插入.

 

/**
     *插入排序(WHILE循环实现)
     */
    void doInsertSort1(int[] src)
    {
       int len=src.length;
       for(int i=1;i<len;i++)
       {  
           int temp=src[i];
           int j=i;
          
           while(src[j-1]>temp)
           {
              src[j]=src[j-1];
              j--;
              if(j<=0)
                  break;
           }
           src[j]=temp;
           printResult(i+1,src);
       }
    }

/**
     *插入排序(FOR循环实现)
     */
    void doInsertSort2(int[] src)
    {
       int len=src.length;
       for(int i=1;i<len;i++)
       {
           int j;
           int temp=src[i];
           for(j=i;j>0;j--)
           {
              if(src[j-1]>temp)
              {
                  src[j]=src[j-1];
                 
              }else//如果当前的数，不小前面的数，那就说明不小于前面所有的数，
                   //因为前面已经是排好了序的，所以直接通出当前一轮的比较
                  break;
           }
           src[j]=temp;
           printResult(i,src);
       }
    }

4.快速排序

通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分关键字小,则分别对这两部分继续进行排序,知道整个序列有序.

把整个序列看做一个数组,把第零个位置看做中轴,和最后一个比,如果比它小交换,比它大不做任何处理,交换了以后再和小的那端比,比它小不交换,比他大交换,这样循环往复,一趟排序完成,左边就是比中轴小的,右边就是比中轴大的,然后再用分治法,分别对这两个独立的数组进行排序.

public int getMiddle(Integer[] list, int low, int high) {
        int tmp = list[low];    //数组的第一个作为中轴
        while (low < high) {
            while (low < high && list[high] > tmp) {
                high--;
            }
            list[low] = list[high];   //比中轴小的记录移到低端
            while (low < high && list[low] < tmp) {
                low++;
            }
            list[high] = list[low];   //比中轴大的记录移到高端
        }
        list[low] = tmp;              //中轴记录到尾
        return low;                   //返回中轴的位置
    }