第三章算法作业

1. 任选作业题”单调递增最长子序列“、”挖地雷“、”编辑距离问题“中的一题分析。

挖地雷

3-3 挖地雷 (25分)

 

在一个地图上有n个地窖（n≤200）,每个地窖中埋有一定数量的地雷。同时，给出地窖之间的连接路径，并规定路径都是单向的,且保证都是小序号地窖指向大序号地窖，也不存在可以从一个地窖出发经过若干地窖后又回到原来地窖的路径。某人可以从任意一处开始挖地雷，然后沿着指出的连接往下挖（仅能选择一条路径），当无连接时挖地雷工作结束。设计一个挖地雷的方案，使他能挖到最多的地雷。

输入格式:

第一行：地窖的个数；

第二行：为依次每个地窖地雷的个数；

下面若干行：

xi yi //表示从xi可到yi，xi<yi。

最后一行为"0 0"表示结束。

输出格式:

k1-k2−…−kv //挖地雷的顺序 挖到最多的雷。

输入样例:

6
5 10 20 5 4 5
1 2
1 4
2 4
3 4
4 5
4 6
5 6
0 0

 

输出样例:

3-4-5-6
34

#include<iostream>
#include<cstring>
#define MAXN 200
using namespace std; 
bool a[MAXN][MAXN];//a[i][j]表示第i个地窖和第j个地窖是否通路
int w[MAXN];//每个地窖的地雷数
int f[MAXN];//f[i]表示从第i个地窖开始挖的最多地雷数
int suf[MAXN];
int main()
{
    long n, i, j, x, y, l, k, maxn;
    cin >> n;
    for(i = 1; i <= n; i++)
    {
        cin >> w[i];
    }
    while(cin >> x >> y)
    {
        if(x == 0 && y == 0)
        break;
        a[x][y] = true;
    }
    f[n] = w[n];//初始状态
    for(i = n - 1; i >= 1; i--) 
    {
        l = 0; 
        k = 0;
        for(j = i + 1; j <= n; j++)
        {
            if(a[i][j] && f[j] > l)
            {
                l = f[j];
                k = j;
            }
        }
        f[i] = w[i] + l;
        suf[i] = k;
    }
    k = 1;
    for(i = 1;i <= n; i++)//从n个数中找最大值 
    {
        if(f[i] > f[k])
        k = i;
     } 
    maxn = f[k];
    cout << k;//先输出起始点
    k = suf[k];
    while(k != 0)
    {
        cout << "-" <<k;
        k = suf[k];
     } 
    cout << endl;
    cout << maxn << endl;
    return 0;
} 

1.1 根据最优子结构性质，列出递归方程式  

f[i] = max{w[i] + f[j]} (a[i][j] > 0, i< j <= n)

1.2 给出填表法中表的维度、填表范围和填表顺序

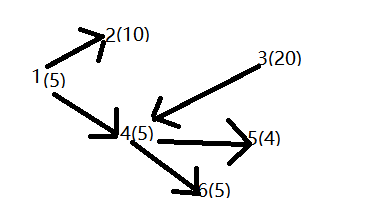
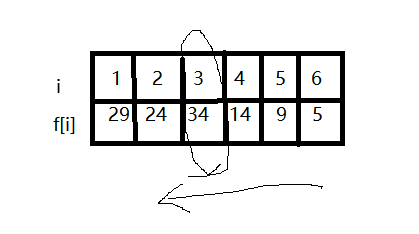
1.3 分析该算法的时间和空间复杂度

时间复杂度O(n^2)

2. 你对动态规划算法的理解

动态规划算法通常可以按以下几个步骤进行：

找出最优解的性质，并刻画其结构特征；

递归地定义最优值；

自底向上方式计算出各子结构的最优值；

根据计算最优值时得到的信息，构造最优解。

步骤1~3是动态规划算法的基本步骤。若需要最优解，则必须执行第4步，为此还需要在第3步中记录构造最优解所必需的信息。

我觉得动态规划在求值时就是得考虑前者后者的关系，还要看其走向是怎样的，首先就得把其递归方程式求出来，根据递归方程确定走向是怎样的，再填表，最后再根据这些步骤写成代码，但是，虽然能理解这些步骤，可是每到做题的时候就又不会了，不知道怎么下手，但听老师讲的时候又突然发现，诶，做法怎么都是一样的。

3. 说明结对编程情况

结对编程这种做法挺好的，既能讨论题目，代码，又能增进感情，不过经常的都是我同伴比我先做出题来，然后我去理解同伴的做法，她很细心，还会写很多注释方便我理解，但是有时我感觉同伴的注释很难理解，很难说服自己，很难让老师明白时，我就很着急了，因为同伴明白这意思，但说出来的意思我理解不了，（说服不了我）结果我说的答案都被老师否决了，而同伴只能干着急，不能为我做些什么，我内心就有点难受，我咋地就不懂呢，我咋滴拖了后腿呢，但是当老师讲了以后我才发现，同伴也理解错了（虽然答案对了）哈哈哈。