1.本周视频学习内容:https://www.bilibili.com/video/BV1Tb411H7uC?p=2
1)P2 概率论与贝叶斯先验
2)P3 矩阵和线性代数
机器学习是一门多领域交叉学科,涉及较多的数学知识,本节课知识之前都有学过,这次根据重点重新梳理一遍,一定要多加重视。通过观看视频,大家对课程的数学基础部分加深印象。
建议大家边看边做笔记,记录要点及所在时间点,以便有必要的时候回看。学习笔记也是作业的一部分。
2.作业要求:
1)贴上视频学习笔记,要求真实,不要抄袭,可以手写拍照。
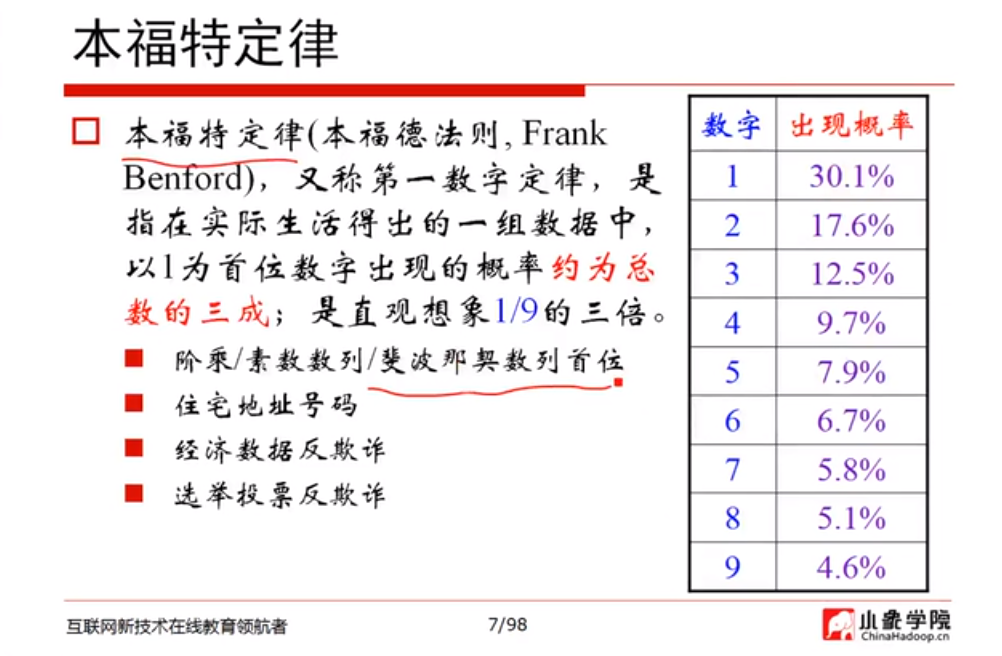
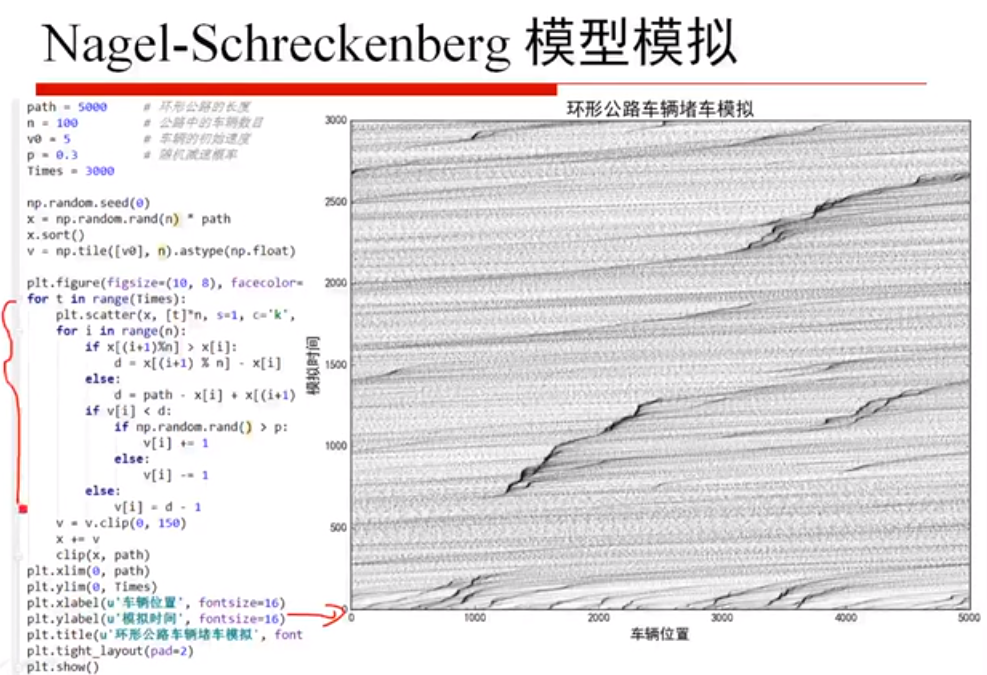
图1 本福特定律 图2 模型模拟


图3 概率公式 图4 贝叶斯公式


图5 两点分布 图6 二项分布


图7 Taylor展式 图8 泊松分布


图9 均匀分布 图10 指数分布


图11 指数分布的无记忆性 图12 正态分布
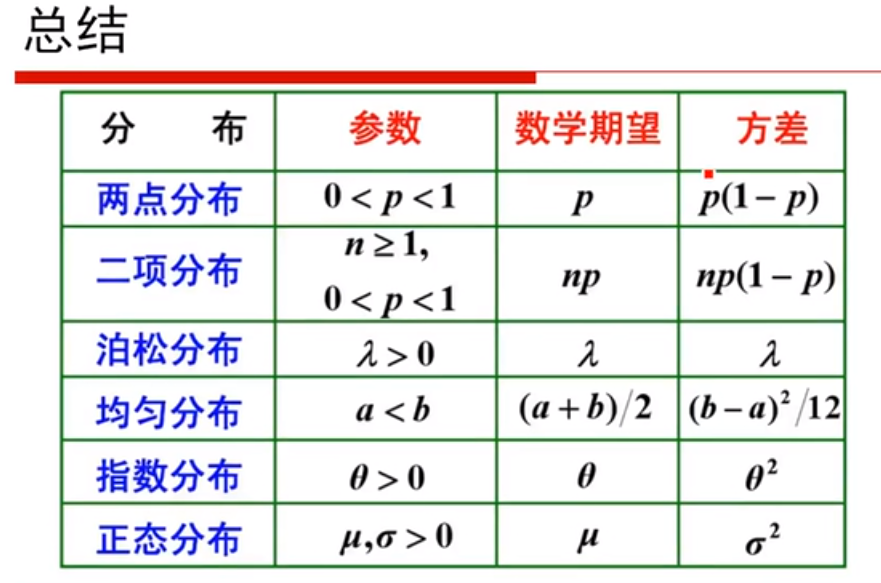

图13 总结 图14 beta分布


图15 beta分布期望 图16 sigmoid函数导数


图17 事件的独立性 图18 期望的性质


图19 方差 图20 协方差


图21 协方差和独立、不相关 图22协方差上界


图23 pearson相关系数 图24 伯努利定理

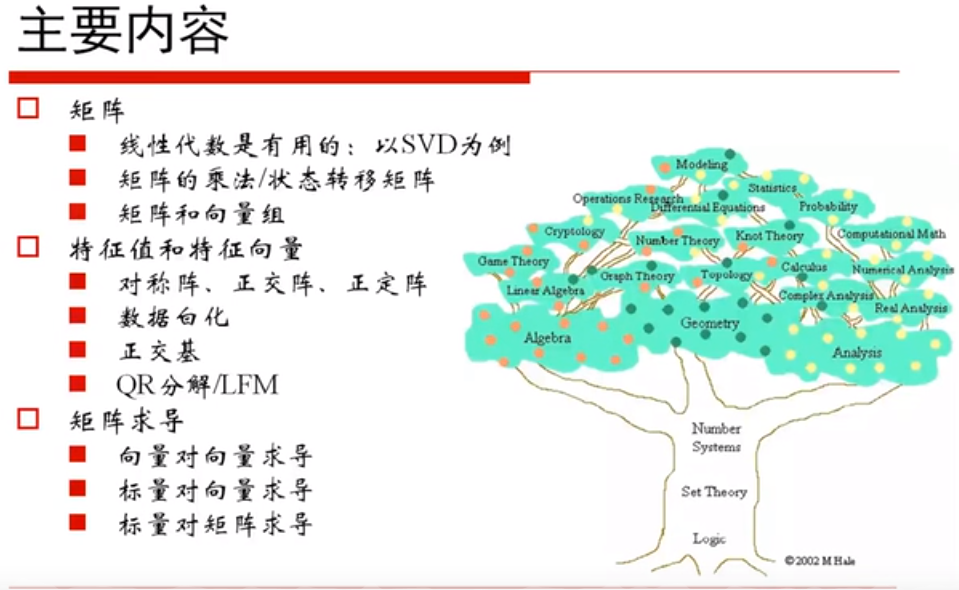
图25 中心极限定理 图26 矩阵学习主要内容


图27 线性代数 图28 代数余子式


图29 范德蒙行列式 图30 概率转移矩阵


图31 矩阵和向量乘法 图32矩阵的秩


图33 秩与线性方程组的解的关系 图34 正交阵
2)用自己话总结“梯度”,“梯度下降”和“贝叶斯定理”,可以word编辑,可做思维导图,可以手写拍照,要求言简意赅、排版整洁。
梯度:梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。一般来说,梯度可以定义为一个函数的全部偏导数构成的向量(这一点与偏导数与方向导数不同,两者都为标量)。最主要的点为梯度向量的方向即为函数值增长最快的方向。
梯度下降:梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数,即无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一,另一种常用的方法是最小二乘法。在机器学习算法中,在最小化损失函数时,可以通过梯度下降法来一步步的迭代求解,得到最小化的损失函数,和模型参数值。简而言之就是得到函数的最优解,机器算法的说法是最小损失函数。
贝叶斯定理:贝叶斯定理也称贝叶斯推理,贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。其中P(A|B)是在B发生的情况下A发生的可能性。简而言之就是用来描述两个条件概率之间的关系,结果与先验条件有很大关系,比如A事件下发生B事件的概率,与B事件下发生A事件的概率是不一样的。