DAY2
依旧是yyx出题
依旧毒瘤
滞空(jump/1s/64M)
题目描述:
pyy在平面上第一象限内发现了顺序n个平台(她可以踩在这些平台上,但必须从第i-1号平台跳跃至i-1号平台),这些平台的横坐标互异且单调递增,从i号平台出发依次跳跃经过2-->n号平台不允许落地。
给出pyy的质量m和重力加速度g(重力沿y轴负方向),考虑理想情况下,求pyy需要消耗的最小能量(不考虑落至平台冲量(即落至平台后速度为0))(单位J)。

设E为能量,m为质量,v为速度,x为位移,a为加速度,t为时间,h为两个点高度差。
能量守恒指在本题中初始动能视为人体能量消耗;
牛顿第二定律给出加速运动中,加速度与位移间关系的公式;
动能定理和重力势能公式给出能量计算公式。

样例输入
3 1 1 2 2 3 3
样例输出
499122214J


一个鬼畜的物理题。。。
pyy在中子星上以光速跳跃???
我自闭了
#include<bits/stdc++.h> using namespace std; typedef long long LL; const LL mod = 998244353; inline void rd(LL &x) { x=0;int f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} } LL n,m,x[2],y[2],g,ans; LL qpow(LL a) { LL res=1,k=mod-2; while(k) { if(k&1)res=res*a%mod; a=a*a%mod; k>>=1; } return res; } LL _2 = qpow(2); void down(LL x,LL h){x%=mod;h%=mod; ans += (x*x*m%mod)*qpow(4*h); ans%=mod;} void up(LL x,LL h) {x%=mod;h%=mod; ans += (m*h%mod) + ( (x*x*m%mod) *qpow(4*h) )%mod; ans%=mod;} void pi_4(LL x){x%=mod; ans += (m*x%mod)*_2; ans%=mod;} void solve() { scanf("%lld%lld%lld",&n,&m,&g); rd(x[1]); rd(y[1]); for(int i=2;i<=n;i++) { rd(x[i&1]); rd(y[i&1]); if(y[i&1]>y[!(i&1)]) up(x[i&1]-x[!(i&1)],y[i&1]-y[!(i&1)]); if(y[i&1]<y[!(i&1)]) down(x[i&1]-x[!(i&1)],y[!(i&1)]-y[i&1]); if(y[i&1]==y[!(i&1)]) pi_4(x[i&1]-x[!(i&1)]); } printf("%lldJ",ans*g%mod); } int main() { freopen("jump.in","r",stdin); freopen("jump.out","w",stdout); solve(); fclose(stdin); fclose(stdout); return 0; }
放爆竹(bomb/1s/64M)
1 题目描述
小明和小辉一起放爆竹。
小辉将很多地雷和春雷穿成了n串。因为地雷和春雷爆炸的声音是不一样的,所以串起来以后,爆炸的声音也是不一样的。
小辉原本想让小明告诉他,如果同时点燃n串雷,最多会有多长的时间至少有两串雷爆炸的声音是一样的。
但是小辉觉得这个问题真是太简单了,所以决定问小明,如果在山谷中(有回音)同时点燃n串雷,那最多会有多长的时间至少有两串雷爆炸的声音是一样的呢?
小辉认为一枚春雷或者地雷爆炸都需要1ms,且山谷中的回音不减弱,并且小辉给出的雷串不会是任意一个雷串的重复(不管重复的雷串是否存在,即无论如何都不会存在类似于 01010101的雷串)。
2 输入
2.1 输入格式
第一行,一个数,表示有n串雷。
接下来n行,其中第i行一个01字符串描述小辉的第i串雷,其中0表示春雷,1表示地雷。
2.2 样例1输入
5 001 1000 0100 010 100
2.3 样例2输入
6 010 011 001 0010011 101 110
3 输出
3.1 输出格式
一行,一个数表示小明给出的答案。
3.2 样例1输出
4
3.3 样例2输出
6
4 样例解释
4.1 样例1解释
第3串雷0100爆炸后得到的声音串0100010001000100…
第4串雷010爆炸后得到声音串010010010010010…
两个声音串的前4位是一样的,所以小辉前4ms听到的声音是一样的。






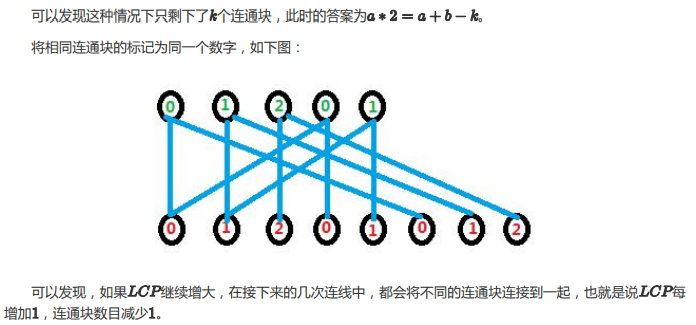

#include <bits/stdc++.h> using std::max; using std::strlen; const int N=20010,Mlen=510,Node=N*Mlen*2; int n,len[N],ans; char s[N][Mlen]; struct Trie{ int son[Node][2],node,app[Node],dep[Node],f[Node]; void init() { son[0][0]=son[0][1]=0; app[0]=dep[0]=0; } int newnode(int d){ ++node; son[node][0]=son[node][1]=0; dep[node]=d; app[node]=0; return node; } void insert(char *s,int len,int t) { int p=0,add=0; while (t) { for (int i=0;i<len && add<=1000;++i) { int &x=son[p][s[i]-'0'],pp=p; p=x?x:x=newnode(dep[p]+1); f[p]=pp; app[p]++; add++; } t--; } } int FindAns() { int ans=0; for (int i=1;i<=node;++i) if (app[i]>=2) { ans=max(ans,dep[i]); } // for (int i=1;i<=node;++i) if (app[i]>=2 && ans==dep[i]) { // int p=i; // while (p) { // putchar((p==son[f[p]][1])+'0'); // p=f[p]; // } // putchar(' '); // break; // } return ans; } }tr; void Init() { scanf("%d",&n); for (int i=1;i<=n;++i) { scanf("%s",s[i]); len[i]=strlen(s[i]); } } void Solve() { tr.init(); for (int i=1;i<=n;++i) { tr.insert(s[i],len[i],(1000-1)/len[i]+1); } printf("%d ",tr.FindAns()); } int main() { freopen("bomb.in","r",stdin); freopen("bomb.out","w",stdout); Init(); Solve(); fclose(stdin); fclose(stdout); return 0; }
以上是正解std
我的菜鸡做法:
也是字典树,先不考虑重复的情况,把n个01串在字典树上建出来,并且多记录一个数组num表示经过某一条边的字符串的数量
然后遍历字典树中num大于1的边,每次遇到结尾的标记end就将这一个字符串重新复制一遍接在现在节点的下方
在遍历的时候记录数量,然后取max就行了
由于这是有需要的时候才复制,应该会比上面的题解快一些吧rwr
#include<cstdio> #include<iostream> #include<cstdlib> #include<iomanip> #include<cmath> #include<cstring> #include<string> #include<algorithm> #include<queue> using namespace std; int n; char s[2005][501]; int ch[20000500][5]; int end[20000050]; int num[20000050]; int cnt,id; int ans; inline void build(int x) { int now=0; for(int i=0;i<strlen(s[x]);i++) { int c=s[x][i]-'0'; if(!ch[now][c]) ch[now][c]=++cnt; now=ch[now][c]; num[now]++; } end[now]=(++id); } void dfs(int now,int an) { ans=max(ans,an); printf("%d ",ans); if(num[now]>1&&end[now]!=0) { int noow=now; for(int j=0;j<strlen(s[end[now]]);j++) { int c=s[end[now]][j]-'0'; if(!ch[noow][c]) ch[noow][c]=++cnt; noow=ch[noow][c]; num[noow]++; } end[noow]=end[now]; } for(int i=0;i<=1;i++) { if(num[ch[now][i]]>1) { if(ch[now][i]==0) continue; else { dfs(ch[now][i],an+1); } } else continue; } } int main() { // freopen("bomb.in","r",stdin); // freopen("bomb.out","w",stdout); scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%s",s[i]); build(i); } num[0]=n; dfs(0,0); printf("%d ",ans); }
pyy整队(queue,1s,128M)
问题描述:
众所周知pyy当了班长,服务于民。一天体育课,趁体育老师还没来,pyy让班里n个同学先排好队。老师不在,同学们开始玩起了手机。站在队伍前端玩手机,前面的人少了,谁都顶不住。于是陆陆续续有人往队伍最后躲去,但大家都沉迷某骗氪手游,忘记了老师说前面位置有空缺要补齐的要求。一些同学还时不时地低头问向指挥队伍的班长pyy,排在自己前面成绩最好的同学是谁,这样自己才能心安理得放心大胆的继续玩手机。
这时老师来了,同学们在可以忽略不计的时间内收好了手机。看着到处充满空缺的队伍,体育老师勃然大怒并借题发挥,以扬体育组声威,限pyy以最快的时间整顿队伍。由于是体育老师,并看不出来队伍的位置后移了,老师只关心队伍是否整齐没有空缺。
老师给了pyy一次移动一名同学的权力,因此pyy无法使用技能“向前看齐”。pyy的哥哥强制要求你帮助pyy回答之前同学们的问题,并告诉pyy在老师来之后,至少移动多少个同学可以使队伍整齐。
输入格式
第一行为两个整数n,m(1<=n,m<=1e5),表示有n位同学,在老师来之前进行了m次小动作。
第二行为n个以空格隔开的整数a1,a2,…,an(1<=ai<=1e7) ,表示初始时队伍中第i位同学的年级成绩排名(数据保证不会有两人成绩重复)。
接下来m行描述同学们的行为,每行由一个字符A或S和一个整数x∈{ai|1<=i<=n} 构成。若为A,x,则表示年级成绩排名为x的同学向pyy询问自己前面成绩最好的是哪位同学;若为M,x,则表示年级成绩排名为x的同学此时躲到了当前队伍的最尾端(不存在队尾同学躲向队尾)。
输出格式
前m个操作中对于每个同学的询问,顺序输出所询问同学的年级成绩排名,并以换行隔开。若询问学生不存在则输出-1。
最后一行输出至少移动多少位同学,使得队伍整齐。
样例输入
4 5 23 150 37 301 A 37 M 23 M 37 A 301 A 37
样例输出
23 150 23 1
数据范围
对于10%的数据 n<=10,m<=20
对于30%的数据 n<=10^3,m<=10^4
对于100%的数据 n<=10^5,m<=10^5,ai<=10^7
正解
离散化成绩+权值线段树维护每个人的位置。每次移动将人的位置移动到n+k(k为操作次数)。
注意一个细节,询问是寻找x前面权值最小的元素,那么需要获取实际情况中pre_x的权值使用链表模拟即可。
最后枚举最终队列的队首,判断长度为n范围外有多少人需要调整。(其实什么方法都可以搞搞)
部分分
对于10%的数据:模拟
对于30%的数据: n^2暴力模拟每个时刻的情况
#include<bits/stdc++.h> using namespace std; typedef long long LL; const LL mod = 998244353; inline void rd(LL &x) { x=0;int f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} } LL n,m,x[2],y[2],g,ans; LL qpow(LL a) { LL res=1,k=mod-2; while(k) { if(k&1)res=res*a%mod; a=a*a%mod; k>>=1; } return res; } LL _2 = qpow(2); void down(LL x,LL h){x%=mod;h%=mod; ans += (x*x*m%mod)*qpow(4*h); ans%=mod;} void up(LL x,LL h) {x%=mod;h%=mod; ans += (m*h%mod) + ( (x*x*m%mod) *qpow(4*h) )%mod; ans%=mod;} void pi_4(LL x){x%=mod; ans += (m*x%mod)*_2; ans%=mod;} void solve() { scanf("%lld%lld%lld",&n,&m,&g); rd(x[1]); rd(y[1]); for(int i=2;i<=n;i++) { rd(x[i&1]); rd(y[i&1]); if(y[i&1]>y[!(i&1)]) up(x[i&1]-x[!(i&1)],y[i&1]-y[!(i&1)]); if(y[i&1]<y[!(i&1)]) down(x[i&1]-x[!(i&1)],y[!(i&1)]-y[i&1]); if(y[i&1]==y[!(i&1)]) pi_4(x[i&1]-x[!(i&1)]); } printf("%lldJ",ans*g%mod); } int main() { freopen("jump.in","r",stdin); freopen("jump.out","w",stdout); solve(); fclose(stdin); fclose(stdout); return 0; }