功能:对于一个排序好的数组,每一个数组的值都代表一个范围也就是前一个数与当前这个数所组成的范围,比如数组0 5 9 10 12 15 45 65 89,下标1所组成的范围为0<x<=5,我们要做的是,给一个值,找到这个数在数组哪个值的范围里,如果在就返回数组这个值的下标,不在返回-1,这里有两种方法,第一种方法使应用遍历的方式,从前往后遍历或者从后往前遍历,找到第一个大于查找值的数,返回其下标
按最坏的时间复杂度估算O(n)第二种就是用二分的思想,按最坏的时间复杂度估算O(logN)这个量级,在这篇博客中我只解释和实现怎么查找这个过程不实现在这个位置进行插入
第一种方法遍历,采用从数组索引0下标开始遍历,并且每次与查找值相比较,,找到第一个大于查找值的数,那么查找值就在这个数所表示的范围里,
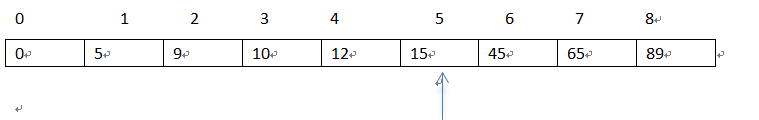
第二种方法采用二分的思想:二分通俗的 讲也就是折半的查找,不管二分的先决条件是数据是按升序或者降序排好的,二分就是思想就是把查找值与数组中的中间值相比较,如果查找值大于中间值,那么就在查找范围就为中间值的右边,继续使用二分,反之,这查找范围为左边,继续使用二分查找;
基于这个思想,加一些条件,我们就可以实现这些功能!
1.如果查找值大于数组的最后一个值,那么直接返回-1
2.如果查找值小于或者等于中间值,并且要比中间值前一个数值大,那么就返回中间值的下标
3.如果查找值大于中间值,并且要中间值后一个数值要小,那么就返回中间值后一个数值的下标
4.如果二分的中间值为第一个数,那么直接返回中间值的下标0(这条可以跟2综合,在代码中,返回二分中间值的下标)
5.如果二分的中间值为最后一个数,那么直接返回中间值的下标(数组的长度-1)(这条可以跟2,4综合,在代码中,返回热分中间值的下标)
6.如果查找值大于中间值并且不会小于中间值的后一个数,那么二分的范围要变动,左边的边界为中间值下标+1,右边边界保持不变
7.如果查找值小于中间值并且不会大于中间值的前一个数,那么二分的范围要变动,右边界为中间值下标-1,左边边界保持不变
举例子,假设要查找的值为20,
图片举例:

这里我只举了一个例子,你可以去找任何一个例子,一定在我综合的7种情况中,
代码示例:
/** * 函数功能:在有一个排好序的数组中,每个数值下标的值与前一个值所组成的一个范围,如果待查找值在这个数组 * 所组成的若干个的一个范围中就返回这个值的下标 * 函数参数:arr排好序的数组,key待查找值 * 函数返回值:待查找值在数组所组成的若干个范围中一个数的下标,如果不再就返回-1 */ public static int binearySeach(int arr[],int key){ int left = 0; //数组的左边界的下标 int right = arr.length-1; //数组的右边界的下标 int mid; //中间值的下标 while(left<=right){ mid = (right+left) / 2;//求中间值的下标 if(arr[right]<key){//第一种情况 return -1; }else if(mid==left||mid==right||arr[mid]>=key&&key>arr[mid-1]){//第2,4,5情况 return mid; //返回中间值的下标 }else if(arr[mid]<key&&key<=arr[mid+1]){//第三种情况 return mid+1; }else if(arr[mid]<key&&key>arr[mid+1]){//第六情况 left = mid + 1;//左边的边界为中间值下标+1,右边边界保持不变 }else{//第7种情况 right = mid -1;//右边界为中间值下标-1,左边边界保持不变 } } return -1; }
还用一种方式是在上面的代码中改成递归的方式!把第六种情况和第七种情况改成调用函数的方式!跟上面的思想大同小异!
代码如下:
/**
* 函数功能:递归版,在有一个排好序的数组中,每个数值下标的值与前一个值所组成的一个范围,如果待查找值在这个数组
* 所组成的若干个的一个范围中就返回这个值的下标
* 函数参数:arr排好序的数组,key待查找值,left数组的左边界的下标,right数组右边界的下标
* 函数返回值:待查找值在数组所组成的若干个范围中一个数的下标,如果不再就返回-1
*/
public static int binearySeach(int arr[],int left,int right,int key){
int mid = (right+left) / 2;//求中间值的下标
if(arr[right]<key){//第一种情况
return -1;
}else if(mid==left||mid==right||arr[mid]>=key&&key>arr[mid-1]){//第2,4,5情况
return mid; //返回中间值的下标
}else if(arr[mid]<key&&key<=arr[mid+1]){//第三种情况
return mid+1;
}else if(arr[mid]<key&&key>arr[mid+1]){//第六情况,进行进行二分,采用递归的方式
return binearySeach(arr,mid+1,right,key);//左边的边界为中间值下标+1,右边边界保持不变
}else{//第7种情况,继续进行二分,采用递归的方式
return binearySeach(arr,left,mid-1,key);//右边界为中间值下标-1,左边边界保持不变
}
}