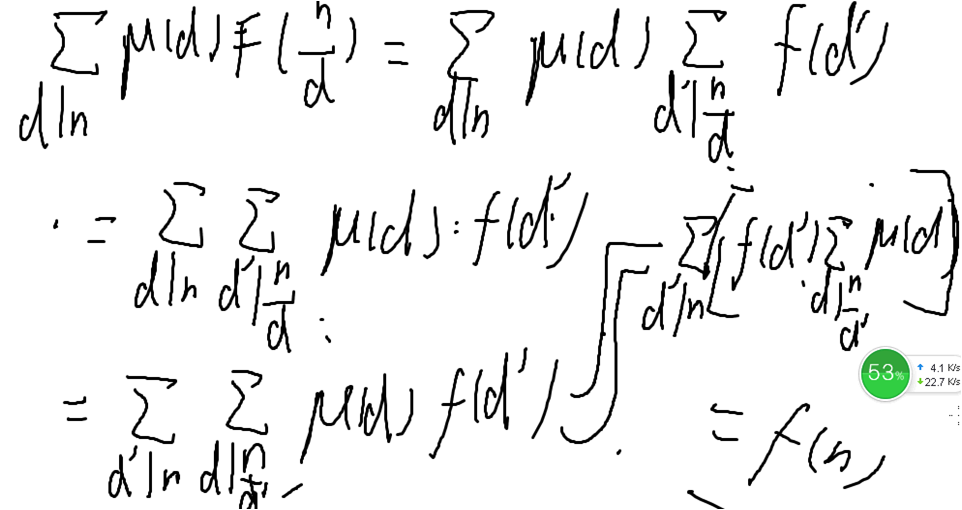1.欧拉定理
设x1,x2,.....,xk,k=φ(n)为1~n中k个与n互质的数
结论一:axi与axj不同余
结论二:gcd(axi,n)=1
结论三:x1,x2,...,xk和ax1,ax2,...,axk一一对应
结论四:aφ(n)≡1(mod n)
计算:φ(m)=m*(1-1/p1)*......*(1-1/pi)
Back to here
请证明:如果n为素数,取a<n,设n-1=d*2r,则要么ad≡1(mod n)要么存在0<=i<r,使得ad*2^t≡-1(mod n),要么存在0<=i<r,使得ad*2^t≡-1(mod n)
证:由费马小定理得an-1≡1(mod n),已知n-1=d*2r
∴ad*2^r≡1(mod n)
∴ad*2^r-1≡0(mod n)
由平方差公式知:(ad*2^(r-1))(ad*2^(r-1))≡0(mod n)
∴原式=(ad-1)(ad+1)(ad*2+1)(ad*2^2).......(ad*2^(r-1)+1≡0(mod n)
2.线性求逆元
求1~n所有数 对p的逆元(p为质数)
为了减少时间,我们要尽量利用已经求出来的逆元进行计算,也就是说,当求i的逆元时,1~i-1的逆元已经求完了
设1<=i<=n
∵p/i=k......r
∴p=ik+r
ik+r≡0 (mod p)
kr-1+i-1≡0 (mod p)
i-1≡-kr-1 (mod p)

最后一步把k和r带进去就可以得到
卡n log n的复杂度用到
3.BSGS算法(baby-step gaint-step)
问题:求ax≡b (mod m)的最小正整数解(m为质数)
如果枚举:复杂度为O(m)
考虑分块

能否从其中某一行找到答案
从第二行找答案等价于第一行里面是否存在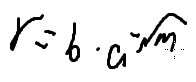
从第三行找答案等价于第二行里面是否存在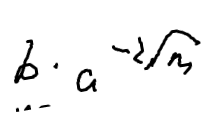
先暴力出第一行,再排序二分,这样求每一行都可以化成第一行
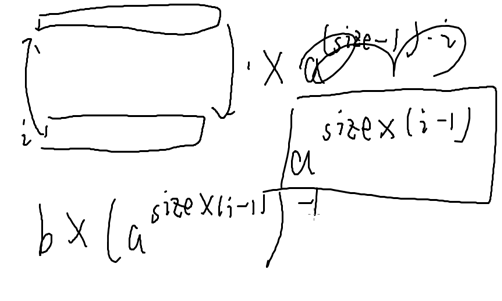
代码如下:
#include<iostream> #include<algorithm> #include<cstdio> #include<cstring> #include<cmath> #include<cstdlib> using namespace std; int size,a,b,p,z[50005]; bool erfen(int x)//二分查找答案 { int l=0,r=size; while (l+1!=r) { int m=(l+r)>>1; if (z[m]>=x) r=m; else l=m; } return z[r]==x; } int powmod(int x,int y,int z) { int i=x; int s=1; while(y) { if(y&1) { s=(s*i)%z; } i=(i*i)%z; y>>=1; } return s%z; } int bsgs(int a,int b,int p)//bsgs算法 { size=sqrt(p);//分块 int nowv=1; for(int i=1;i<=size;i++) { nowv = (long long) nowv*a%p;//枚举 z[i] = nowv; if(z[i]==b) return 1; } sort(z+1,z+size+1); for(int i=2;(i-1)*size+1<=p;i++) { int y=(long long)b*powmod(powmod(a,size*(i-1),p),p-2,p); if(erfen(y)) { for(int j=(i-1)*size+1;j<=i*size;j++) if(powmod(a,j,p)==b) return j; } } return -1; } int main() { cin>>a>>b>>p; cout<<bsgs(a,b,p); return 0; }
i-1行*size个数+1
4.数论函数
喂正整数吐整数
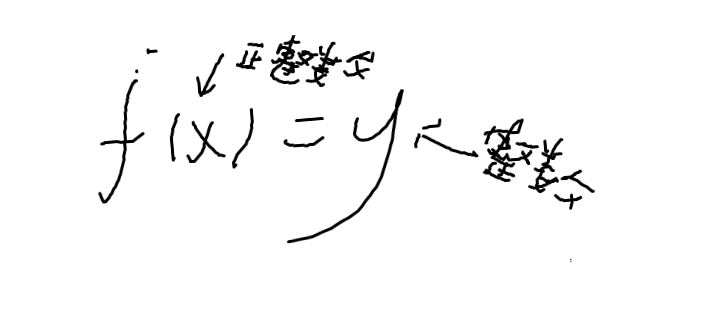
积性函数
积性函数:当gcd(a,b)=1时,ƒ(ab)=ƒ(a)ƒ(b)
完全积性函数:ƒ(ab)=f(a)f(b)
积性函数包括:
不变函数:ƒ(n)=n
欧拉函数:ƒ(n)=φ(n)
莫比乌斯函数:ƒ(n)=μ(n)
因子数目总数:ƒ(n)=d(n)
因子之和函数:ƒ(n)=σ(n)


如μ(4)=0
μ(15)=1
μ(1001)=-1
φ和μ的实现:考虑线性筛,降低复杂度
代码如下:
memset(not_prime,0,sizeof(not_prime)); for (int i=2;i<=n;i++) { if (!not_prime[i]) { prime[++ prime_cnt] = i; phi[i] = i-1; mu[i] = -1; } for (int j=1;j<=prime_cnt;j++) { int x = i * prime[j]; if (x>n) break; not_prime[x] = true; phi[x] = phi[i] * phi[prime[j]]; mu[x] = mu[i] * mu[prime[j]]; if (i % prime[j] == 0) { phi[x] = phi[i] * prime[j]; mu[x] = 0; break; } } }