今天又是长者给我们讲小学题目的一天
长者的讲台上又是布满了冰红茶的一天
-------------------------------------------------------------------------------------------------------------------------------------
正片开始
动态规划
动态规划是个抽象的东西。
接下来的例子小部分可能会比较搞笑
我们先来看一个严肃的例子,来认识一下什么是DP:
斐波那契数列:
大家都知道斐波那契数列是个啥吧
就是这个: f(0)=0,f(1)=1,f(n)=f(n-1)+f(n-2)
它和DP有什么关系呢?
1.都要有边界条件(这里就是f(0)=0,f(1)=1)
2.都有转移方程(这里的是f(n)=f(n-1)+f(n-2))
3.都有当前状态(这里就是f(n))
这样我们也就总结出来了做DP要注意的东西:
1.定义状态
2.定义边界
3.转移方程
以上也是做DP的步骤。
代码的几种写法:
顺着推,逆着推,记忆化搜索
//以斐波那契数列为例的三种写法 int dfs(int n) { if(n==0)f[0]=0; else if(n==1)f[1]=0; if(vis[n])return f[n]; vis[n]=true; f[n]=dfs(n-1)+dfs(n-2); return f[n]; } int main() {int n,f[100]; //逆着推(无优化) vis[0]=1;vis[1]=1; cin>>n; f[0]=0; f[1]=1; for(int i-2;i<=n;i++) f[i]=f[i-1]+f[i-2]; cout<<f[n]; //顺着推 cin>>n; f[0]=0;f[1]=1; for(int i=0;i<n;i++) {f[i+1]+=f[i]; f[i+2]+=f[i]; } //记忆化搜索 cin>>n; cout<<dfs(n)<<endl; }
noip的考纲虽然比宇宙还大,但是总会有那么几种常考的东西。
常考DP:
数位DP
树形DP
区间DP
状压DP
其它DP(这个是最常考的)
一.数位DP
举个栗子
读入两个正整数l,r,求从l到r之间一共有多少个数?
ans=r-l+1
但是只有这么一句不优雅,所以我们要用数位DP做。
ans=[0,r]的数-[0,l]的数
这样我们就把问题转化为求[0,x]区间上的数了。我们先把x的十进制表示出来。
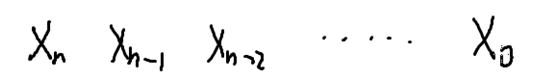
其中X0代表个位,X1代表十位.....以此类推
我们这个题实际上是求满足0<=v<=x的v
我们对v进行相同的操作
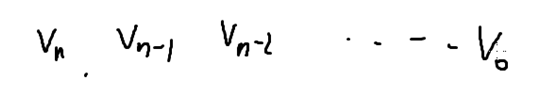
如果当v不足n位时,就是有前导0.我们在每一位上填上0~9之间的一个整数,看满足要求的v有多少。我们从高位开始填。那这就会有很多种情况对不对?我们举个例子分析一下
假如我们要填Vn-3,那么按照从高位开始填的顺序,Vn,Vn-1,Vn-2已经填好了。我们把每个Vi和每个Xi比较一下。

我们把这些数分到两边。
①.左边>右边 那Vn-3就随便填了
②.左边<右边 填的Vn-3就必须<=Xn-3,当然这里还有个坑,我们待会程序里讲
我们用f[i][j]表示已经填到了第i位,j表示V的第i-1位及以前是否等于X的i-1位及以前,这种情况下的方案数。(0是不等于,1是等于),ans=f[0][0]+f[0][1]。
转移:对于每个f[i][0],f[i][0]=9*f[i-1][0]+(X(n-i)-1)*f[i-1][1](后面这一部分是指前i-1位都等于,第i位不等于)
f[i][1]=f[i-1][1],因为永远等于x的数不会变
边界:f[n+1][1]=1 因为Vn+1=Xn+1=0
int f[100][2]; int solve(int x) { int z[100]; int n; while(x) {z[n++]=x%10; x/=10; } n--; memset(f,0,sizeof(f));//要记住清空以防意外 f[n+1][1]=1;//Xn+1与Vn+1都是0,所以是等于(顶上界)的情况 for(int i=n;i>0;i--) for(int j=0;j<=1;j++) { if(j==0) { for(int k=0;k<=9;k++) f[i][0]+=f[i+1][j];//把f[i][j]的方案数加到f[i][0]上 (注意不是+9) 用循环的方式加起来方便以后改程序 } else { for(int k=0;k<=z[i];k++) {if(k==z[i])f[i][1]+=f[i+1][j];//如果顶上界,就加到f[i][1](顶上界的数组)(左边=右边)里面 else f[i][0]+=f[i+1][j];//如果当前位填的数<z[i],就说明不顶上界,就加到f[i][0]里面 } } } return f[0][0]+f[0][1]; } int main() {int l,r; cin>>l>>r; cout<<solve(r)-solve(l-1)<<endl; }
上面说的顶上界就是Vi=Xi的情况(私下的称呼,懒的改了)
绕了好大一圈解决了一个简单题

数位之和:例如123,数位之和=1+2+3=6
这里把上一个题改一改,再加一个数组记录数位之和即可(i,j的意义不变)
int f[100][2];//方案数之和,j=0:不顶上界,j=1:顶上界 int g[100][2];//数位之和 int solve(int x) { int z[100]; int n; while(x) {z[n++]=x%10; x/=10; } n--; memset(f,0,sizeof(f)); memset(g,0,sizeof(g)); f[n+1][1]=1; g[n+1][1]=0; for(int i=n;i>0;i--) for(int j=0;j<=1;j++) { if(j==0) { for(int k=0;k<=9;k++)//枚举每个要填的数 {f[i][0]+=f[i+1][j];//每一个方案的后面都+k,那对总的数位之和的贡献就是f[i+1][j](方案数)*k(新填的数) g[i][0]+=g[i+1][j]+f[i+1][j]*k } } else { for(int k=0;k<=z[i];k++) {if(k==z[i]) {f[i][1]+=f[i+1][j]; g[i][1]+=g[i+1][j]+f[i+1][j]*k; } else {f[i][0]+=f[i+1][j]; g[i][0]+=g[i+1][0]+f[i+1][j]*k; } } } } return f[0][0]+f[0][1]; } int main() {int l,r; cin>>l>>r; cout<<solve(r)-solve(l-1)<<endl; }

这个题多了一个限制条件。
多加一个维度肯定能把这题做出来。
-------------------长者
那我们就多加一个维度好了。
状态: 因为我们要比较相邻两个数位上的数,又是从高位向低位填写,所以只需要记录当前填的最后一位。
因为我们要比较相邻两个数位上的数,又是从高位向低位填写,所以只需要记录当前填的最后一位。
作业1:洛谷P2657windy数(咕咕咕)
树形DP:
我们看一道简单的不行的题
给定一棵有n个点的树,请问这棵树有几个点?
答案是n个点吗?真的是n个点吗?当然是啦
好我们想想这题怎么做
先介绍一下树。
树最上面的点叫根,最下面的点叫叶子结点。
子树:由一个结点向下走,能走到的所有结点构成的树叫以这个结点为根的子树。
有多少个点:以根节点为根的子树的点。f[i]:以i这个点为根的子树的点的个数,这里就要求f[1]。
边界:f[叶子结点]=1
转移:f[p]=f[ls[p]]+f[rs[p]]+1.左儿子+右儿子+1=p结点的子树大小
长者只放了伪代码qwq

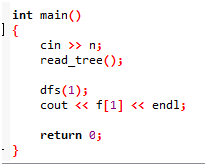
对了这个题的答案是n,所以这个题只要读入n,再输出就好辣。
我们来看点有档次的东西
给一个n个点的树,求直径(距离最远的两个点的距离)
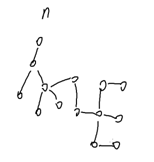
首先,每种路径都长这个样子(这里指一个点到另一个点)
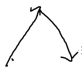
我们把它换个方向
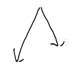
是不是顺眼了?这样就符合从一个结点向下走的方向了。
既然每种路径都长这样,那直径一定长这样喽。
从一个点找两种尽量长(最长+次长)的路径拼起来就是以这个点为拐点的最长一条路径。
我们用f[i][0]表示从点i向下走,最长的路径长度,f[i][1]表示从点i向下走,次长路径的长度。
状态转移便是选择儿子。
f[p][0]=max{f[p1][0],f[p2][0]...f[pk][0]}+1求最大值:必定走儿子中路线最长的那个,再加上1(用一 步到达儿子)
f[p][1]:假如我们刚才选了pi,f[p][1]=max{f[p1][0],...(把f[pi][0],f[pi][1]去掉)}+1
ans=f[1][0]+f[1][1];
状压DP
状压就是状态压缩。
为什么要状态压缩呢?
看个例子:
给n个点,坐标分别为(x1,y1),(x2,y2).........(xn,yn)(这不是个图,你可以乱走)一个人在一号点,从1号点出发,把剩下的点至少走一次,使走过的路径最短(TSP问题(中文:旅行商问题))
经典的Np-hard问题(最快也是2^n级别)
1.每个点只去一次
2.最短就是走线段
假如我们已经走了1,2,5
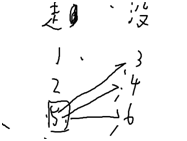
3,4,6每个点都可行。(只是不一定最短)

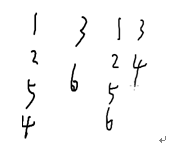
这里每个走过/没走过都是集合,so我们怎么表是成数组下标?
这里就是状态压缩了(集合--->数)。用二进制即可完成。
构造n位(元素的个数)二进制数,每位用0/1来表示某个元素是否在集合里。(0为不在,1为在)
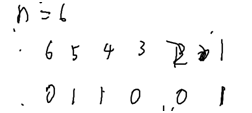
例如这个二进制数与{1,4,5}等价.
TSP问题:f[s][i],s为n位二进制数,(已经走过的点所对应的集合)已经走过s里的所有点,现在停留在i点的最小距离。
边界:f[1][1]=0.
枚举要走的点j。(要保证j不属于s这个集合)
--->f[ { s∪j } ][ j ]=f[ s ][ j ]+dis[ i ][ j ](从点i走到点j)
转移:实际上是把走过的点的元素变多==>把二进制上的0不断边1==>s变大
所以按s从小到大枚举
//状压dp int n,f[100],x[100],y[100]; double dis(int x,int y)//算距离 { return sqrt((x[x]-x[y])*(x[x]-x[y])+(y[x]-y[y])*(y[x]-y[y])); } double f[1<<maxn][maxn];//s表示一个集合转换成二进制数,一个n个点,所以最大为2^n int main() {cin>>n; for(int i=0;i<n;i++)//0~n-1方便二进制 cin>>x[i]>>y[i]; for(int i=0;i<(1<<n);i++) for(int j=0;j<n;j++) f[i][j]=1e+20; f[1][0]=0;//为了对应二进制,起点变为0 for(int s=1;i<(1<<n);s++)//枚举全部可能的点的集合 {for(int i=0;i<n;i++)//枚举停留点,要注意is是否在s里面 {if((s>>i)&1)//判断也就是s的第i位是否是1 {for(j=0;j<n;j++)//枚举要走哪个点 if(((s>>j)&1)==0)//j不能走过 f[s|(1<<j)][j]=min(f[s|(1<<j)][j],f[s][i]+dis(i,j)); //f的第一维就是把j放到s集合里。 } } } //最后枚举所有可能停的点中最小的一个 double ans=1e+20; for(int i=0;i<n;i++) ans=min(ans,f[(1<<n)-1][i]);//n个1组成的所有的数:2^n-1 cout<<ans<<endl; }
说点数据范围的事儿
n<=20(22):状压 n<=12:O(n!) n<=32(50)直接放弃 (来自长者的建议) n<=100:n^3(Floyd,区间) n<=1000:O(n^2) n<=10^5:数据结构 n<=10^6:O(n) n>10^6:O(1)/O(log n)
区间DP:
合并石子:有n堆石子,可以合并相邻两堆。合并代价是这两堆的数目之和。把n堆石头合并为一堆,求最小代价。
把相邻的两堆合为一堆:区间dp
区间dp形式:f[l][r]代表把第l堆石子到第r堆石子合并为一堆的最小代价,求f[1][n]
边界:f[i][i]=0
转移:因为最后一次合并,一定是把某堆和另一堆合并为一堆。合并时不改变原来石头的顺序,所以合并的那两堆一定对应某个分界线,如下图:
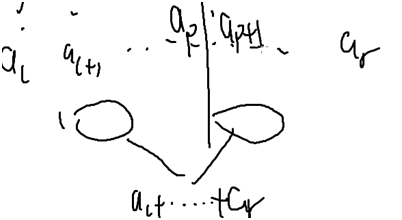
左边那一堆:f[l][p],右边那一堆:f[p+1][r].
so f[l][r]=min(f[l][p]+f[p+1][r]+sum[l][r])注意别忘加黄色部分。(区间和)这里我们枚举p)
int f[100][100]; int main() {int n,z[100]; cin>>n; for(int i=1;i<=n;i++) cin>>z[i]; make_sum(); memset(f,0x3f,sizeof(f));//将f数组初始化为非常大的数 (最好不用0x7f,因为两个加起来爆int) for(int i=1;i<=n;i++) f[i][i]=0;//只有一堆:代价为0 //我们需要枚举左端点,右端点,断点 for(int l=1;l<=n;l++) for(int r=l+1;r<=n;r++)//r从l+1开始,因为r=l算完了 for(int p=l;p<r;p++) f[l][r]=min(f[l][r],f[l][p]+f[p+1][r]+sum[l][r]);//sum[l][r]用前缀和算一下 //好了上面的那段是错的,但是为什么? //问题在于执行顺序。在算f[1][r]时f[2][r],f[3][r]....都没有算过 //每一个大区间都由两个小区间得来,所以我们在最外层枚举区间长度 for(int len=2;len<=n;len++) for(int l=1;r=len;r<=n;l++,r++)//区间整体向右移动 for(int p=l;p<r;p++) f[l][r]=min(f[l][r],f[l][p]+f[p+1][r]+sum[l][r]); cout<<f[1][n]; //复杂度O(n^3),so n也就最多200多 }
如果我们把这n堆弄成个环,改怎么弄呢
a1,an 相邻处理方法:
ans=min(f[1][n],f[2][n+1])
但是a1,a2就不相邻了.....
考虑考虑,全部加完之后:
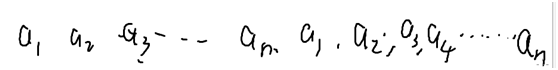
最终答案ans=min(f[i][n+i-1])
为什么呢?因为把一个环合成一个点,一定会有一条边用不到(合并相当于减少一条边)那我们把那条用不掉的边去掉。这里选择答案的过程就是枚举去掉哪条边
一些普通DP

我们用 f[i][j]:到第i行第j列的方案数
边界: f[1][j]=f[i][1]=1
转移:f[i][j]=f[i-1][j]+f[i][j-1];
小结论:左上角-->右下角
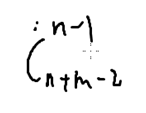
一共n+m-2步,向右走n-1步

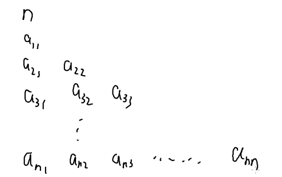
每次向下/右下走
权值:路径上所有数的和。要找权值最大的路径的值
f[i][j]:从(1,1)走到(i,j)的最大权值
f[1][1]=a[1][1]
f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j]从左上和正上走过来
改造版:
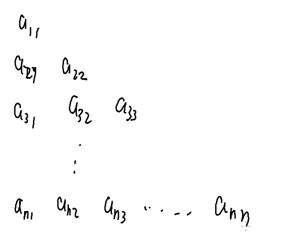
找到一条路径,使这条路的权值之和在模m之后最大
n,m<=100 数据比较x小---->给大了做不了/m也是个维度
(之前最优解不一定是之后最优解--->加维度)
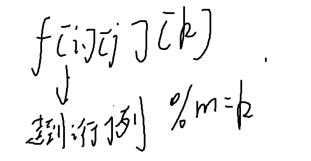
f[i][j][k]:
1,1到i,j 的权值和mod m=k是否可能存在
因为走到i,j之前的权值之和是k-aij,所以f[i][j][k]=f[i-1][j-1][(k-aij)mod m ] or f[i-1][j][k-aij]
边界:f[1][1][a11%m]=1
ans=最后一行最大的可能的k

f[i]表示以ai结尾的最长上升子序列的长度
枚举i前面的j<i,aj<ai,f[i]=max(f[j])+1
O(n^2)(T掉一半)
数据增强到10^5:用线段树。f[i]=max(f[j])+1(1<=j<i,aj<ai)
假设v=max(a1.........an)
建一棵长度为v的线段树

按值左右划分,所有f[i]<ai(对应的f)的数都在ai左边按照f[i]大小排序
轻松找出fj最大值,+1得到fi,然后修改,利用线段树进行区间询问最大值和单点修改
稍微特殊一点的DP:
背包:背包九讲qwq
01背包: 有n个物品,第i个的价值为wi,体积为vi.有一背包大小为m,在放入的物品体积之和不超过m的情况下,价值之和最大。这是最基本的问题。叫01背包是因为每个物品要么放进背包,要么不放进背包
f[i][j]表示判断完第1到i个物品,占用j体积的最大价值。
f[ i+1 ][ j ](第i+1个物品不放)=f[ i ][ j ]
f[ i+1 ][ j+v[ i+1 ] ](第i+1个物品放)=f[ i ][ j ]+w[ i+1 ]
完全(无穷)背包:有n个物品,第i个的价值为wi,体积为vi.有一背包大小为m,每种物品无数个,问最大权值。
把循环倒过来qwq
策略1:枚举每种用多少个 f[i][j]+x*w[i+1]àf[i+1][j+x*v[i+1]]
复杂度:
策略二:消掉枚举:f[i][j]=max(f[i-1][j],f[i][j-v[i]]+w[i])
第i个物品选0个 又选了一次第i个物品
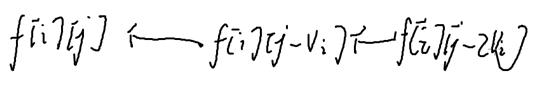
告诉每个物体有多少个:直接枚举
一些练习:

用数位DP。
显然要加一维
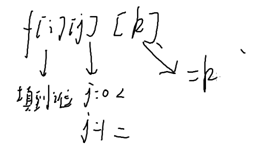
第三维记录乘积
但是k最大到9^18,总之空间会炸。
k不能为11(1~9的质因子只有2,3,5,7)
k可以写成如下形式:
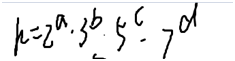
so,
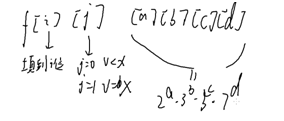
虽然它有6维,但它不会炸
因为a+b+c+d<=log210^18+log310^18+log510^18+log710^18