小木棍
题目描述
乔治有一些同样长的小木棍,他把这些木棍随意砍成几段,直到每段的长都不超过5050。
现在,他想把小木棍拼接成原来的样子,但是却忘记了自己开始时有多少根木棍和它们的长度。
给出每段小木棍的长度,编程帮他找出原始木棍的最小可能长度。
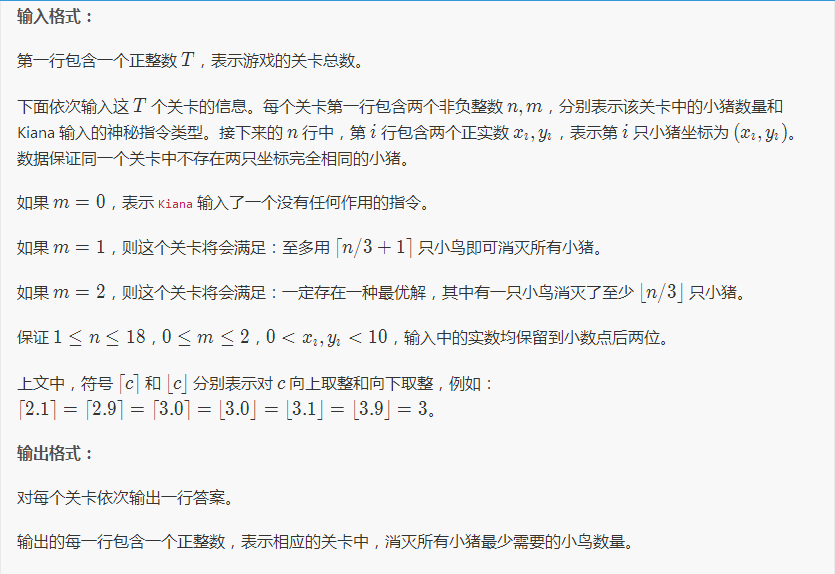
输入输出格式
输入格式:
共二行。
第一行为一个单独的整数N表示砍过以后的小木棍的总数,其中N≤65N≤65
(管理员注:要把超过5050的长度自觉过滤掉,坑了很多人了!)
第二行为NN个用空个隔开的正整数,表示NN根小木棍的长度。
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 #include<vector> 7 #include<queue> 8 #include<map> 9 #include<set> 10 #include<stack> 11 using namespace std; 12 const int maxn=100007; 13 const int INF=0x7f7f7f7f; 14 int n,m,sum,stp,ans=INF,req; 15 int len[maxn],s[maxn],nxt[maxn]; 16 bool is[maxn],usd[maxn],bj; 17 void gettable(){ 18 for(int i=2;i<=sqrt(sum);i++){ 19 if(sum%i==0){ 20 if(i>=len[1]) s[++stp]=i; 21 if(i!=(sum/i)) if(sum/i>=len[1]) s[++stp]=sum/i; 22 } 23 } 24 } 25 bool cmp(int a,int b){ 26 return a>b; 27 } 28 /*bool dfs(int now,int st,int lft){ 29 bool flg=false; 30 if(lft==0&&st==sum/req) return true; 31 if(lft==0){ 32 int i; 33 for(i=1;i<=n;i++){ 34 if(!usd[i]){usd[i]=true;flg=true;break;} 35 } 36 if(flg) dfs(i,st+1,req-len[i]); 37 } 38 bool flag=false; 39 for(int i=now+1;i<=n;i++){ 40 if(usd[i]) continue; 41 if(lft>=len[i]){ 42 usd[i]=true;flag=true; 43 if(dfs(i,st,lft-len[i])) return true; 44 else return false; 45 usd[i]=false; 46 } 47 } 48 if(!flag) return false; 49 }*/ 50 void dfs(int k,int last,int rest){ 51 int i,j; 52 if(rest==0){ 53 if(k==(sum/req)){bj=1;return;} 54 for(i=1;i<=n;i++) 55 if(!usd[i]){usd[i]=true;break;} 56 dfs(k+1,i,req-len[i]); 57 usd[i]=false; 58 if(bj) return; 59 } 60 int l=last+1, r=n, mid; 61 while(l<=r){ 62 mid=(l+r)/2; 63 if(len[mid]<=rest) r=mid-1; 64 else l=mid+1; 65 } 66 for(i=l;i<=n;i++){ 67 if(!usd[i]){ 68 usd[i]=1; 69 dfs(k,i,rest-len[i]); 70 usd[i]=0; 71 if(bj) return; 72 if(rest==len[i]) return; 73 i=nxt[i]; 74 if(i==n) return; 75 } 76 } 77 } 78 int main(){ 79 cin>>m; 80 for(int i=1;i<=m;i++){ 81 int a;cin>>a;if(a>50) continue; 82 len[++n]=a;sum+=len[n]; 83 } 84 sort(len+1,len+n+1,cmp); 85 gettable(); 86 sort(s+1,s+n+1,cmp); 87 nxt[n]=n; 88 for(int i=n-1;i>=1;i--){ 89 if(len[i]==len[i+1]) nxt[i]=nxt[i+1]; 90 else nxt[i]=i; 91 } 92 for(int i=1;i<=stp;i++){ 93 if(is[i]) continue; 94 memset(usd,false,sizeof(usd)); 95 bj=false;usd[1]=true;req=s[i]; 96 dfs(1,1,req-len[1]); 97 if(!bj){ 98 for(int j=i+1;j<=stp;j++){ 99 if(s[i]%s[j]==0) is[j]=true; 100 } 101 } 102 else ans=min(ans,s[i]); 103 } 104 if(ans==INF) cout<<sum<<endl; 105 else cout<<ans<<endl; 106 }
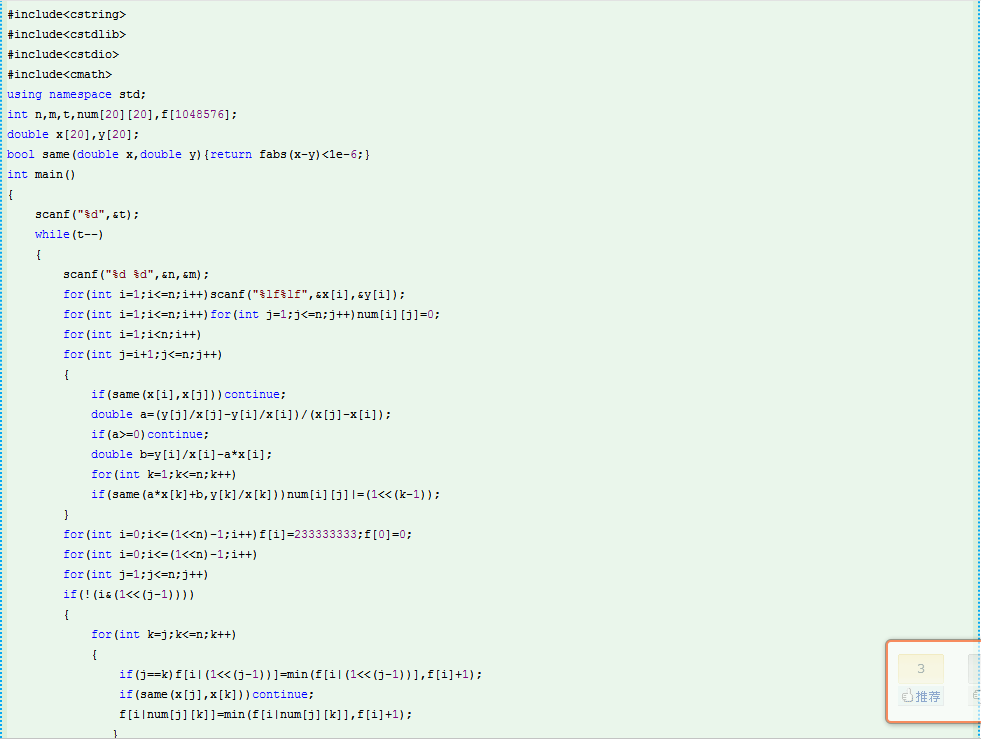
愤怒的小鸟

这样搜会T一半的点:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 using namespace std; 7 typedef long double dd; 8 const int maxn=27; 9 const int INF=0x7f7f7f7f; 10 const dd eps=1e-8; 11 int t,n,m,ans; 12 dd x[maxn],y[maxn]; 13 bool flag,bflg[maxn][maxn]; 14 bool usd[maxn],busd[maxn][maxn][maxn]; 15 dd geta(dd x1,dd x2,dd y1,dd y2){ 16 dd ret; 17 ret=(x1*y2-y1*x2)/((x1*x2)*(x2-x1)); 18 return ret; 19 } 20 dd getb(dd x1,dd x2,dd y1,dd y2){ 21 dd ret; 22 ret=(y2*x1*x1-y1*x2*x2)/((x1*x2)*(x1-x2)); 23 return ret; 24 } 25 void cpy(int zhu,int niao){ 26 for(int i=1;i<=n;i++) 27 busd[zhu][niao][i]=usd[i]; 28 bflg[zhu][niao]=flag; 29 } 30 void recpy(int zhu,int niao){ 31 for(int i=1;i<=n;i++) 32 usd[i]=busd[zhu][niao][i]; 33 flag=bflg[zhu][niao]; 34 } 35 bool zai(dd x,dd y,dd a,dd b){ 36 dd tmp=a*x*x+b*x; 37 if(fabs(tmp-y)<eps) return true; 38 return false; 39 } 40 void dfs(int zhu,int niao){ 41 if(niao>ans||niao>n) return; 42 if(m==1){ 43 int tmp; 44 if(n%3!=0) tmp=n/3+1+1; 45 else tmp=n/3+1; 46 if(niao>tmp) return; 47 } 48 if(m==2){if(zhu<(n/3)&&!flag) return;} 49 if(zhu==0){ 50 if(m==0) ans=min(ans,niao); 51 if(m==1) ans=min(ans,niao); 52 if(m==2){ 53 if(flag) ans=min(ans,niao); 54 } 55 } 56 for(int i=1;i<=n;i++){ 57 if(usd[i]) continue; 58 bool vis=false; 59 for(int j=i+1;j<=n;j++){ 60 if(!usd[i]&&!usd[j]){ 61 dd a=geta(x[i],x[j],y[i],y[j]); 62 dd b=getb(x[i],x[j],y[i],y[j]); 63 if(a<=0){ 64 int tmp=zhu; 65 cpy(zhu,niao); 66 for(int k=1;k<=n;k++){ 67 if(usd[k]) continue; 68 if(zai(x[k],y[k],a,b)){ 69 usd[k]=true;tmp--; 70 } 71 } 72 if((zhu-tmp)>=(n/3)) flag=true; 73 vis=true;dfs(tmp,niao+1); 74 recpy(zhu,niao); 75 } 76 } 77 } 78 if(!vis){ 79 usd[i]=true;dfs(zhu-1,niao+1); 80 usd[i]=false; 81 } 82 } 83 } 84 int main(){ 85 //freopen("a.in","r",stdin); 86 scanf("%d",&t); 87 while(t--){ 88 ans=INF;flag=false;memset(usd,false,sizeof(usd)); 89 memset(x,0,sizeof(x));memset(y,0,sizeof(y)); 90 scanf("%d%d",&n,&m); 91 for(int i=1;i<=n;i++) cin>>x[i]>>y[i]; 92 dfs(n,0);if(ans==INF) ans=n; 93 printf("%d ",ans); 94 } 95 }
这样搜比较好:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 #include<cmath> 6 using namespace std; 7 typedef double dd; 8 const int maxn=27; 9 const int INF=0x7f7f7f7f; 10 const dd eps=1e-8; 11 int t,n,m,ans; 12 dd x[maxn],y[maxn],ai[maxn],bi[maxn],xi[maxn],yi[maxn]; 13 bool zai(dd x,dd y,dd a,dd b){ 14 dd tmp=a*x*x+b*x; 15 if(fabs(tmp-y)<eps) return true; 16 return false; 17 } 18 bool tong(dd x,dd y){ 19 return fabs(x-y)<eps; 20 } 21 dd geta(dd x1,dd x2,dd y1,dd y2){ 22 dd ret; 23 ret=(x1*y2-y1*x2)/((x1*x2)*(x2-x1)); 24 return ret; 25 } 26 dd getb(dd x1,dd x2,dd y1,dd y2){ 27 dd ret; 28 ret=(y2*x1*x1-y1*x2*x2)/((x1*x2)*(x1-x2)); 29 return ret; 30 } 31 void dfs(int z,int u,int v){ 32 if(u+v>=ans) return; 33 if(z>n){ans=min(ans,u+v);return;} 34 bool vis=false; 35 for(int i=1;i<=u;i++){ 36 if(zai(x[z],y[z],ai[i],bi[i])){ 37 vis=true;dfs(z+1,u,v);break; 38 } 39 } 40 if(!vis){ 41 for(int i=1;i<=v;i++){ 42 dd xx=xi[i];dd yy=yi[i]; 43 if(tong(xx,x[z])) continue; 44 dd a=geta(x[z],xx,y[z],yy); 45 dd b=getb(x[z],xx,y[z],yy); 46 if(a<0){ 47 ai[u+1]=a;bi[u+1]=b; 48 dd tm=xi[i];dd tp=yi[i]; 49 for(int j=i;j<v;j++){ 50 xi[j]=xi[j+1];yi[j]=yi[j+1]; 51 } 52 dfs(z+1,u+1,v-1); 53 for(int j=v;j>i;j--){ 54 xi[j]=xi[j-1];yi[j]=yi[j-1]; 55 } 56 xi[i]=tm;yi[i]=tp; 57 } 58 } 59 xi[v+1]=x[z];yi[v+1]=y[z]; 60 dfs(z+1,u,v+1); 61 } 62 } 63 int main(){ 64 //freopen("a.in","r",stdin); 65 scanf("%d",&t); 66 while(t--){ 67 scanf("%d%d",&n,&m);ans=INF; 68 memset(ai,0,sizeof(ai));memset(bi,0,sizeof(bi)); 69 memset(xi,0,sizeof(xi));memset(yi,0,sizeof(yi)); 70 for(int i=1;i<=n;i++) scanf("%lf%lf",&x[i],&y[i]); 71 dfs(1,0,0);printf("%d ",ans); 72 } 73 }
正解是状压: