因为有大佬写的比我更长更具体,所以我也就写写总结一下了
引入:
众所周知,很多图中有个东西名叫环。
对于这个东西很多算法都很头疼。(suchas 迪杰斯特拉)
更深层:环属于强联通分量(strongly connected components):
定义:如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量。
例如:(画画技艺高超到自闭)
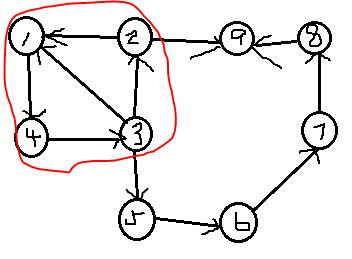
红圈内部即为强联通分量。
对于这个东西,其他算法更难搞;
那么我们为了把这个东西合为一个,或者找出属于一个强联通分量的所有元素,或者其他某些操作,一个叫tarjan的人研发了一个tarjan算法。
为他正名:tarjan,自己听怎么读。
对于tarjan算法求强联通分量,步骤:
1.定义两个数组dfn和low,
dfn[x]表示x节点是第几个被遍历到的。
low[x]表示x以及它的所有子树的出边的dfn的最小值。
2,我们用一个栈来存储遍历到的点,把当前搜到的点的入栈标记in记为true。
3,对于每一个当前节点的子节点,如果之前没有遍历到,就往下遍历,并在遍历后取low的min值:low[x]=min(low[x],low[v])。如果遍历到之前已经遍历到的,也就是in[v]=1,那么我们就不再往下继续搜了,直接传递dfn的值:low[x]=min(low[x],dfn[v]);
4,如果当前节点的dfn的值等于low的值,由于low表示当前节点以及其所有子树的出边的最小dfn的值,那么我们就可以认为low被传递了一圈又回到了当前dfn,也就代表找到了一个强联通分量,那么我们就把从当前的栈顶一直到当前元素的栈中元素全部弹出并作为强联通分量的一部分。
算法主体框架完毕,本质为深搜。
特别的,一个节点也算一个强联通分量,因为它能自己到自己。。。
上代码:
void tarjan(int u){ dfn[u]=++ind; low[u]=dfn[u];//dfn和low初始化,low的初始值为当前dfn,low可以被其子节点更新。 s[top++]=u;//s代表栈,用来存强联通分量。 in[u]=1;//in入栈标记,为bool数组 for(int i=head[u];i;i=e[i].next){//链式前向星存图 int v=e[i].to;//出边 if(dfn[v]==0){//如果没有到过 tarjan(v);//继续往下搜 low[u]=min(low[u],low[v]);//更新low的值 }else{//bian li dao le, v bu zai zi shu li mian if(in[v]){//zai zhan li mian low[u]=min(low[u],dfn[v]);//更新,但是为什么为dfn而不是low,下文详解 } } } if(dfn[u]==low[u]){//为强联通分量的根节点 cnt_scc++;//用来标记为当前强联通分量的编号 while(s[top]!=u){//不断弹出一直弹到当前节点 top--; in[s[top]]=0; scc[s[top]]=cnt_scc;//tarjan主要作用,标记当前点属于第几个强联通分量(也可以作为缩点) } } }
那么,洛谷p2002这道题也就很好做了。
思路:
显然,对于每一个强联通分量内部来说,只要有一个点能够被传送到消息,那么其他点都能被传送到消息。
那么我们将所有强联通分量缩为一个点,然后统计所有强联通分量的入度,如果为0那么答案就需要加一来保证当前强联通分量以及它的子节点们能够被传递到信息。
code:
#include<cstdio> #include<iostream> using namespace std; int n int m; int fro; int t; int sccnum=0; int ru[100001];//表示 i这个强联通分量有无入度(bool也可以) int num=0; int ans=0; int dfn[100001]; int low[100001]; int head[100001]; int stack[100001]; int top; int cnt=0; int belong[100001]; bool in[100001]; struct edge{ int to,next; }edg[500002]; inline int read()//自研快读 { int ans=0; char ch=getchar(),last=' '; while(ch<'0'||ch>'9')last=ch,ch=getchar(); while(ch>='0'&&ch<='9')ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); return last=='-'?-ans:ans; } inline void add(int from,int to)//链式存图 { num++; edg[num].to=to; edg[num].next=head[from]; head[from]=num; } void tarjan(int x)//主体部分 { stack[top++]=x; dfn[x]=low[x]=++cnt; in[x]=1; for(int i=head[x];i;i=edg[i].next) { int v=edg[i].to; if(!dfn[v]) { tarjan(v); low[x]=min(low[x],low[v]); } else if(in[v]) { low[x]=min(low[x],dfn[v]); } } if(dfn[x]==low[x]) { sccnum++; while(stack[top]!=x) { top--; in[stack[top]]=0; belong[stack[top]]=sccnum;//标记为一个强联通分量 } } } int main(){ n=read(),m=read(); for(int i=1;i<=m;i++) { fro=read(),t=read(); if(fro!=t)add(fro,t); } for(int i=1;i<=n;i++)//对每一个点跑一个tarjan { if(!dfn[i])tarjan(i); } for(int i=1;i<=n;i++) { for(int j=head[i];j;j=edg[j].next)//遍历每一个点统计强联通分量入度 { int v=edg[j].to; if(belong[i]!=belong[v])ru[belong[v]]=1; } } for(int i=1;i<=sccnum;i++)//如果入度为0,答案加一 { if(!ru[i])ans++; } printf("%d",ans);//完结 return 0; }
文章主体部分完结。
关于dfn和low的争议:在low取min的时候,为什么不用low[v]而用dfn[v]?
这个也是争论很久的问题,其中著名北大金牌dms就犯错犯过一段时间并且毫无察觉直到他做一个题WA掉。。。
我的理解是这样的。
我们注意到low的定义:low[x]是x的子树里最小的dfn。
如果已经访问过,那么它一定是当前节点的祖先。
如果用low的话那么它也就不再符合定义。
用dfn的话不影响low的传递。因为low是传递一圈最终传递回强联通分量的根节点,用dfn并不影响它祖先的low值传递向其他边,只是作为一个low传递路径的完结标记。(十分感性理解)。
况且在算割点的时候用low的话就把整个强联通分量同化了(low是层层传递的,感性理解),那么求割点的正确性就发生了变化。所以low是不正确的。
当然,因为图论题数据比较难造,有些题目数据不强导致你用low就可以过。况且用low的话对缩点影响不如割点大。
upd in 2020.7.9
从网上找到了一个反例:
假设按以下顺序dfs,括号里表示的是回溯的过程
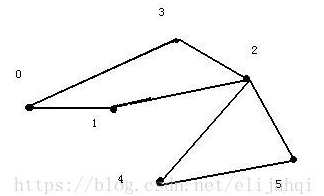
0-1-2-3-0(-3-2)-4-5-2(-5-4-2)-5(-2-1-0)-3(-0)
low和dfn比较:low[0]=low[1]=low[2]=low[3]=0
low[4]=low[5]=2
low和low比较:全部都是0…
问题出在low[5]上,如果是low[5]和dfn[2]比较low[5]=2,如果是和low[2]比较,low[5]=0
当low[5]=2的时候,2判断是割点,当low[5]=0的时候,2判断就不是割点了。
https://blog.csdn.net/elijahqi/java/article/details/80614953(原博文链接)
以上是原作者讲解。
tarjan缩点的本质在于用low进行标记操作。不管是low[v]还是dfn[v],都会使得low[now]和dfn[now]不同。也就满足了tarjan缩点的条件。
但是如果在缩点或者割边的题目中用low[v]去更新,low[v]更新会不符合定义,进而导致以上的错误,也就使得割点判断出错。
完结辣。
对各位有帮助理解的话顶一个吧。