1.无向图邻接矩阵


以上是一个无向图的邻接矩阵,矩阵七个维度的顺序分别是A,B,C,F,L,J,M,假设矩阵第一行第二列为1代表节点A和节点B有连线,显然邻接矩阵此时应为对称矩阵,且对角线元素均为0。若是有权网络,那么矩阵的元素由1变为权重即可无连接则用无穷大Inf代表,实际操作可用65536等较大的数字表示。
2.有向图邻接矩阵
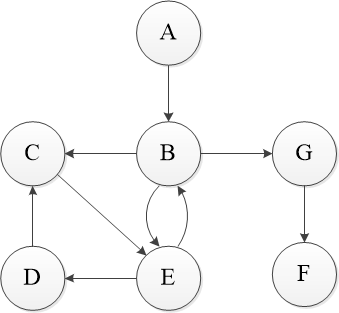

与有向图基本相同,只是无向图中有一条边连接两个点,那么矩阵(i,j)位置的元素和(j,i)的元素应该是相同的,但是有向图矩阵(i,j)位置表示从节点i为弧头,至节点j为弧尾。当然有向图的邻接矩阵不会一定是对称矩阵。
3.无向图的邻接表

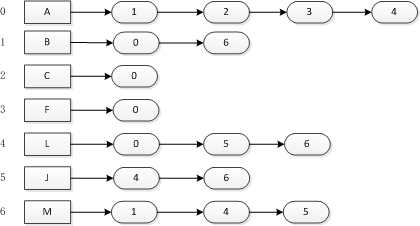
每个顶点拥有一个链表,然后链表的元素包括该点通过边连接的点的序号。【这里的序号其实就是节点数组中的下标】
4.有向图的邻接表

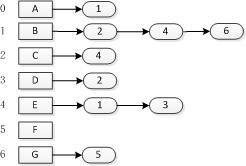
当边稀疏情况下,使用邻接表比邻接矩阵更节省空间。
邻接表任一顶点的下一个邻接点较为方便,但是判断两个点之间是否存在边或弧不及邻接矩阵方便
5.其他的存储方式
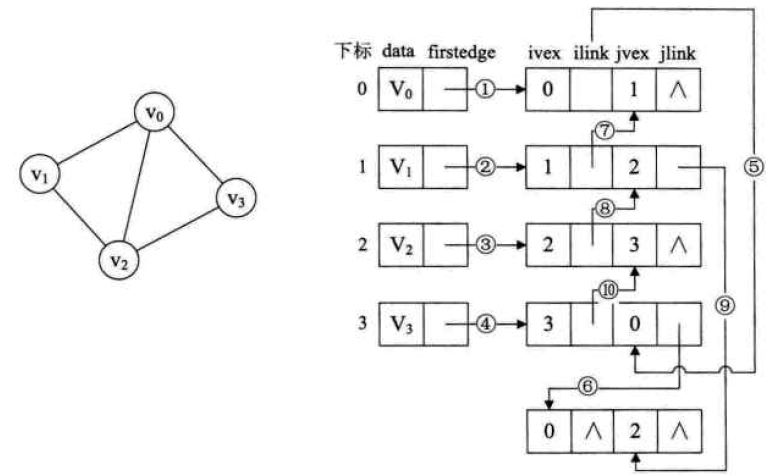
主要是十字链表(Orthogonal List)和邻接多重表(Adjacency Multilist)。这两个是为了解决邻接表存在那些问题,而十字链表主要针对有向图,邻接多重表针对无向图。
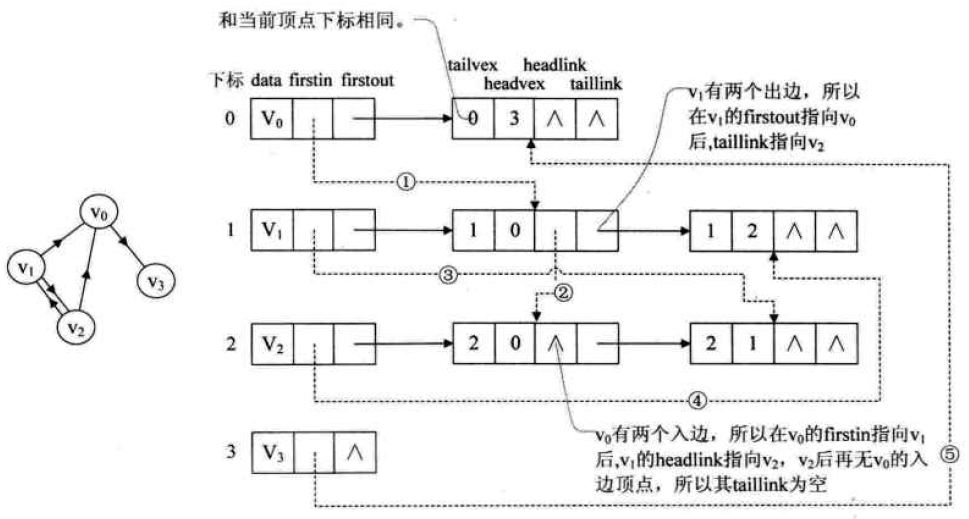
6.问题
那么邻接表该如何表示有权图(网络)呢?
这个问题研究的人就比前面少很多了。