参考自:
数字图像处理第三版,冈萨雷斯
图像处理基础(8):图像的灰度直方图、直方图均衡化、直方图规定化(匹配) - Brook_icv - 博客园 https://www.cnblogs.com/wangguchangqing/p/7098213.html
直方图规定化,又叫直方图匹配。理想情况下,直方图均衡化实现了图像灰度的均衡分布,提高了图像对比度、提升了图像亮度。在实际应用中,有时并不需要图像的直方图具有整体的均匀分布,而希望直方图与规定要求的直方图一致,这就是直方图规定化。
通过一个灰度映像函数,将原灰度直方图改造成所希望的直方图,把图像变换为某一特定的灰度分布,也就是其目的的灰度直方图是已知的。这其实和均衡化很类似,均衡化后的灰度直方图也是已知的,是一个均匀分布的直方图;而规定化后的直方图可以随意的指定,也就是在执行规定化操作时,首先要知道变换后的直方图,这样才能确定变换函数。规定化操作能够有目的的增强某个灰度区间,相比于,均衡化操作,规定化多了一个输入,但是其变换后的结果也更灵活。
在理解了上述的均衡化过程后,直方图的规定化也较为简单。可以利用均衡化后的直方图作为一个中间过程,然后求取规定化的变换函数。具体步骤如下:
- 将原始图像的灰度直方图进行均衡化,得到一个变换函数s=T(r),其中s是均衡化后的像素,r是原始像素
- 对规定的直方图进行均衡化,得到一个变换函数v=G(z)v=G(z),其中v是均衡化后的像素,z是规定化的像素
- 上面都是对同一图像(变换前的待规定化图像和变换后的规定化结果图像)的均衡化,其结果应该是相等的,s=v,且z=G−1(v)=G−1(T(r)),这个公式就是r和z的关系
通过,均衡化作为中间结果,将得到原始像素 r 和 z 规定化后像素之间的映射关系。
详解规定化过程
对图像进行直方图规定化操作,原始图像的直方图和以及规定化后的直方图是已知的。
假设Pr(r)表示原始图像的灰度概率密度,Pz(z)表示规定化图像的灰度概率密度(r和z分别是原始图像的灰度级,规定化后图像的灰度级)。
- 对原始图像进行均衡化操作,则有
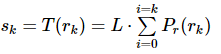
- 对规定化的直方图进行均衡化操作,则
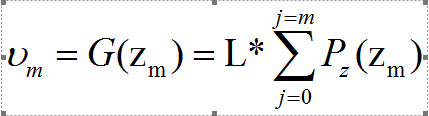
- 由于是对同一图像的均衡化操作,所以有

-
规定化操作的目的就是找到原始图像的像素sk到规定化后图像像素的zm之间的一个映射。
有了上一步的等式后,可以得到sk=G(zm),因此要想找到sk对应的zm只需要在z进行迭代,找到使式子G(zm)−sk的绝对值最小即可。
- 上述描述只是理论的推导过程,在实际的计算过程中,不需要做两次的均衡化操作,具体的推导过程如下:


上面公式表示,假如sk规定化后的对应灰度是zm的话,需要满足的条件是sk的累积概率和zm的累积概率是最接近的
下面是一个具体计算的例子:

首先得到原直方图的各个灰度级的累积概率Vs以及规定化后直方图的各个灰度级的累积概率Vz,那么确定sk到zm之间映射关系的条件就是:
∣Vs−Vz∣的值最小。
以k=2为例,其原始直方图的累积概率是:0.65,在规定化后的直方图的累积概率中和0.65最接近(相等)的是灰度值为5的累积概率密度,则可以得到原始图像中的灰度级2,在规定化后的图像中的灰度级是5。
直方图规定化的实现
直方图规定化的实现可以分为一下三步:
- 计算原图像的累积直方图
- 计算规定直方图的累积直方图
- 计算两累积直方图的差值的绝对值
- 根据累积直方图差值建立灰度级的映射
具体代码
"""直方图规定化,又叫直方图匹配""" import numpy as np import matplotlib.pyplot as plt import cv2 # 定义函数,计算直方图累积概率 def histCalculate(src): row, col = np.shape(src) hist = np.zeros(256, dtype=np.float32) # 直方图 cumhist = np.zeros(256, dtype=np.float32) # 累积直方图 cumProbhist = np.zeros(256, dtype=np.float32) # 累积概率probability直方图,即Y轴归一化 for i in range(row): for j in range(col): hist[src[i][j]] += 1 cumhist[0] = hist[0] for i in range(1, 256): cumhist[i] = cumhist[i-1] + hist[i] cumProbhist = cumhist/(row*col) return cumProbhist # 定义函数,直方图规定化 def histSpecification(specImg, refeImg): # specification image and reference image spechist = histCalculate(specImg) # 计算待匹配直方图 refehist = histCalculate(refeImg) # 计算参考直方图 corspdValue = np.zeros(256, dtype=np.uint8) # correspond value # 直方图规定化 for i in range(256): diff = np.abs(spechist[i] - refehist[i]) matchValue = i for j in range(256): if np.abs(spechist[i] - refehist[j]) < diff: diff = np.abs(spechist[i] - refehist[j]) matchValue = j corspdValue[i] = matchValue outputImg = cv2.LUT(specImg, corspdValue) return outputImg img = cv2.imread('F:program_studyPythondatacity.tif', cv2.IMREAD_GRAYSCALE) # 读入参考图像 img1 = cv2.imread('F:program_studyPythondataLena.tif', cv2.IMREAD_GRAYSCALE) cv2.imshow('input', img) cv2.imshow('refeImg', img1) imgOutput = histSpecification(img, img1) cv2.imshow('output', imgOutput) cv2.waitKey(0) cv2.destroyAllWindows() fig = plt.figure('整个过程直方图显示', (8, 8)) plt.subplot(311) plt.plot(histCalculate(img), 'r', lw=1, label='待匹配累积概率直方图') plt.legend(loc='best') plt.subplot(312) plt.plot(histCalculate(img1), 'b', lw=1, label='参考累积概率直方图') plt.legend(loc='best') plt.subplot(313) plt.plot(histCalculate(imgOutput), 'g', lw=1, label='规则化后的概率直方图') plt.legend(loc='best') plt.show()
局部的直方图处理
除了全局的直方图处理外,还有局部直方图处理。它可以增前图像中小区域的细节。过程是定义一个领域模板,并将模板中心从一个像素移至另一个像素。在每个位置,计算领域中的点的直方图,均衡化或规定化,并将局部的中心元素的作为图像的当前值。