不匹配数据划分的偏差和方差
存在的问题
估算学习算法的偏差和方差,真的可以帮你确定接下来应该优先做的方向。
但是当你的训练集来自和开发/测试集不同分布的时候,分析偏差和方差的方式可能不一样。
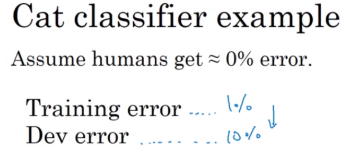
训练集的误差:在得到最终的神经网络之后,将其应用到训练集的每个样本,只进行正向传播,然后得到的错误率。
如果开发集和训练集同分布,你可能会说,这里存在很大的方差问题。你的算法不能从训练集很好地泛化,它处理训练集很好,但处理开发集就突然间效果很差了。
但如果你的训练数据和开发数据来自不同的分布,那么我们就不能简单地下这个结论。特别是,也许算法在开发集上做的不错,可能因为训练集都是高分辨率图片,很容易识别,但开发集要难以识别得多。
所以也许神经网络本身没有方差问题,这只不过反应了开发集包含更难准确分类的问题。
所以这个分析的问题在于,当你看训练误差,再看开发误差,有两个事情改变了:
算法只见过训练集数据,没见过开发集数据。
开发集数据来自不同的分布。
因为我们同时改变了两件事,所以很难确认这增加的9%的误差,有多少是因为算法本身的方差问题,有多少是因为训练、测试集的数据不同分布。
训练-开发集的引入
为了分辨这两个因素的影响,定义一组新的数据是有意义的,我们称之为训练-开发集(training-dev set)
得到训练-开发集的方法为:随机打散训练集(randomly shuffle the training set),然后分出一部分作为训练-开发集。
这样,我们有了训练集、和训练集不同分布的开发集和测试集(但二者同分布)、和训练集同分布的训练-开发集。
神经网络的训练方式+区分方差偏差和数据不匹配
我们只在训练集来训练神经网络(不让神经网络在训练-开发集上跑后向传播),之后我们看神经网络在训练集、训练-开发集、开发集上的误差。
在上方左边例子中,我们可以得出模型方差过大的问题(high variance),即神经网络在训练集表现良好,但无法泛化到同分布的训练-开发集上(也就是同分布但没见过的数据)。
在上方右边的例子中,我们可以看到训练-开发集的误差与训练集的误差差不多,说明方差的问题已经很小了,现在的问题是数据不匹配(data mismatch)的问题(很好理解)。
对于下方左边的例子,训练集的误差就很大,说明模型存在偏差过大的问题(high bias),或者叫可避免偏差问题。
当然,以上三个问题也可能同时存在多个。比如下方右边的例子,同时存在高偏差和数据不匹配的问题。
判断问题所在的几个重要参数

左边从上到下依次为
- human level 人类的表现
- training set error 训练集错误率
- training-dev set error 训练-开发集错误率
- dev error 开发集错误率
- test error 测试集错误率
availible bias 可避免误差=训练集错误率 - 人类的表现
训练-开发集错误率 - 训练集错误率 表现了方差 (variane) 的大小
开发集错误率 - 训练-开发集错误率 表现了数据不匹配(数据不同分布)的程度
测试集错误率 - 开发集错误率 表现了开发集过拟合的程度 如果这俩差距过大,说明开发集过拟合了,所以需要一个更大的开发集。 要注意 开发集和测试集需要同一分布
下面以一个例子介绍一下怎么分析误差
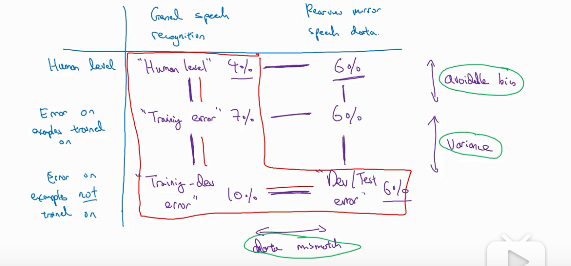
还是那个调动后视镜的语音识别的例子。
这个表格的左上方的是一般的语音识别,右上边的是调动后视镜的语音识别。 一般的语音识别下方是依次是人类错误率、训练集错误率、训练-开发集错误率。后视镜语音识别下边的依次是人类错误率、训练集错误率、开发/测试集错误率。
Human level反映了人类识别这些的难度,对于一般的语音人类错误率为4,后视镜语音为6,说明对人类来说后视镜语音更难识别。 其他的数据之间的分析方法与之前说的一样。