前言
说实话,我感觉这是一个大坑,不知道为什么要设计成这样混乱的形式。
(2020年4月12日更新)过了几年回头看这篇博客,连我自己都看的头发都乱了,又重新理了一遍才把自己说通。。于是这篇博客又被我大改了一遍。
在我用的时候,以row_major矩阵,并且mul函数以向量左乘矩阵的形式来绘制时的确能够正常显示,并不会有什么感觉。但是也有人会遇到明明传的矩阵没有问题,却怎么样都绘制不出的情况;或者使用一遍矩阵,在mul函数用向量左乘的形式却又可以绘制出来的疑问。因此本文目的就是要扫清这些障碍。
ps. 本问题由淡一抹夕霞提供。
DirectX11 With Windows SDK完整目录
欢迎加入QQ群: 727623616 可以一起探讨DX11,以及有什么问题也可以在这里汇报。
一些线性代数基础
行主序矩阵与列主序矩阵
首先要了解的是,对于连续内存数据:
行主序矩阵是这样解释数据的:
而列主序矩阵是这样解释数据的:
显然,行主序矩阵经过一次转置后就会变成列主序矩阵
矩阵左乘与右乘
由于矩阵乘法不满足交换律,则需要区分当前矩阵位于乘号的左边还是右边。有时候经常都会听到左乘和右乘这两个概念,下面是有关它们的含义:
左乘指的是该矩阵位于乘号的左边,例如:行向量 左乘 矩阵,即行向量在乘号的左边
右乘指的是该矩阵位于乘号的右边,例如:列向量 右乘 矩阵,即列向量在乘号的右边
ps. 向量也是矩阵
行向量v和矩阵M满足下面的关系:
C++和HLSL中矩阵的内存布局
在C++的DirectXMath中,无论是XMFLOAT4X4,还是使用函数生成的XMMATRIX,都是采用行主序矩阵的解释方式。它的数据流如下:
上述数据流传递到HLSL后,若是传递给cb0的寄存器的前4个向量,那么它内存布局一定如下:
cb0[0].xyzw = (m11, m12, m13, m14);
cb0[1].xyzw = (m21, m22, m23, m24);
cb0[2].xyzw = (m31, m32, m33, m34);
cb0[3].xyzw = (m41, m42, m43, m44);
而在HLSL中,默认的matrix或float4x4采用的是列主序矩阵的解释形式。
假设在HLSL的cbuffer为:
cbuffer cb : register(b0)
{
(row_major) matrix g_World;
}
如果g_World是matrix或float4x4类型,由于是列主序矩阵,上面的4个寄存器存储的数据会被看作:
而如果g_World是row_major matrix或row_major float4x4类型,则为行主序矩阵,上面的4个寄存器存储的数据则依然被视作:
HLSL中的mul函数
微软的官方文档是这么描述mul函数的(微软官方文档链接),这里进行个人翻译:
使用矩阵数学来进行矩阵x左乘矩阵y的运算,要求矩阵x的列数与矩阵y的行数相等。
如果x是一个向量,那么它将被解释为行向量。
如果y是一个向量,那么它将被解释为列向量。
表面上看起来很美满,很智能,但稍有不慎就要在这里踩大坑了。
dp4指令
dp4是一个汇编指令(微软官方文档链接),使用方法如下:
dp4 dst, src0, src1
其中 src0和src1是一个向量,计算它们的点乘并将结果传给dst。
当然这里并不是要教大家怎么写汇编,而是怎么看。
为了了解mul函数是如何进行向量与矩阵的乘法运算,我们需要探讨一下它的汇编实现。这里我所使用的是row_major矩阵。首先是向量作为第一个参数的情况:
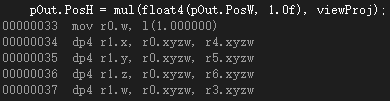
可以看到这种运算方式实际上却是按照向量右乘矩阵的形式进行的运算。
然后是将向量作为第二个参数的情况(仅单纯的参数交换):
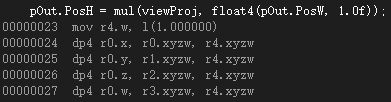
无论是行向量左乘矩阵,还是列向量右乘矩阵,在汇编层面上都是用dp4的形式进行计算,这是因为对矩阵来说在内存上是以4个行向量的形式存储的,传递一行的寄存器向量比传递一列更简单,适合进行与列向量的运算,并且效率会更高。
然后眼尖的同学会发现,同一条指令,只是改变了顺序,指令执行的起始地址就产生了差别(16条指令数目差)。
但是交换两个参数又会导致运算结果/显示结果的不同,这时候就要看看矩阵所存的值了。
先看一段HLSL代码:
cbuffer cb : register(b0)
{
row_major matrix gWorld;
row_major matrix gView;
row_major matrix gProj;
}
struct VertexPosNormalTex
{
float3 PosL : POSITION;
float3 NormalL : NORMAL;
float2 Tex : TEXCOORD;
};
struct VertexPosHWNormalTex
{
float4 PosH : SV_POSITION;
float3 PosW : POSITION; // 在世界中的位置
float3 NormalW : NORMAL; // 法向量在世界中的方向
float2 Tex : TEXCOORD;
};
// 顶点着色器
VertexPosHWNormalTex VS(VertexPosNormalTex pIn)
{
VertexPosHWNormalTex pOut;
row_major matrix viewProj = mul(gView, gProj);
pOut.PosW = mul(float4(pIn.PosL, 1.0f), gWorld).xyz;
pOut.PosH = mul(float4(pOut.PosW, 1.0f), viewProj);
pOut.NormalW = mul(pIn.NormalL, (float3x3) gWorldInvTranspose);
pOut.Tex = pIn.Tex;
return pOut;
}
我们只考虑viewProj的初始化和pOut.PosH的赋值操作。
首先是viewProj经过计算后应该得到的值:

这是向量左乘矩阵开始前四个向量寄存器的值(默认HLSL):

这是向量右乘矩阵开始前时四个向量寄存器的值(将float4(pOut.PosW, 1.0f)和viewProj交换):
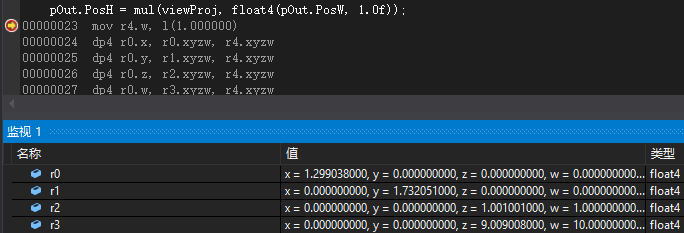
也许有人会奇怪,怎么在开始运算前两边寄存器存储的内容会不一样。我们需要往前观察上一个语句产生的汇编(默认HLSL):

而将float4(pOut.PosW, 1.0f)和viewProj交换后,则汇编代码没有了转置操作:

严格意义上说,00000000到0000001B的指令才是上图语句的实际执行内容,而0000001C到0000002B的代码则应是在计算pOut.PosH = mul(float4(pOut.PosW, 1.0f), viewProj);之前所进行的一系列额外操作。
因此无论是行向量还是列向量,在执行完0000001B指令后,行主序矩阵viewProj的内存布局一定为:

如果用行向量左乘该行主序矩阵,由于dp4运算需要按列取出这些寄存器的值,为此需要额外16条指令进行转置(0000001C到0000002B)。
而如果用列向量右乘该行主序矩阵,则不需要进行转置,直接取寄存器行向量就可以直接进行dp4运算。
因此,我们可以知道一个行向量左乘行主序矩阵时,为了满足mul函数使用dp4指令优化运算,需要会预先对原来的矩阵进行转置。其中r4 r5 r6 r3为viewProj转置后的矩阵,即将会左乘向量float4(pOut.PosW, 1.0f)。而列向量右乘行主序矩阵则可以避免转置操作。
同理,如果采用列主序矩阵,行向量左乘列主序矩阵可以避免转置操作;而列向量右乘行主序矩阵又会产生转置操作。
故对于dp4来说,最好是能够对一个行向量和列主序矩阵(取列主序矩阵的行,也就是取一行寄存器向量与行向量做点乘)操作,又或者是对一个行主序矩阵(取行主序矩阵的行与列向量做点乘)和列矩阵操作,这样都能有效避免转置。
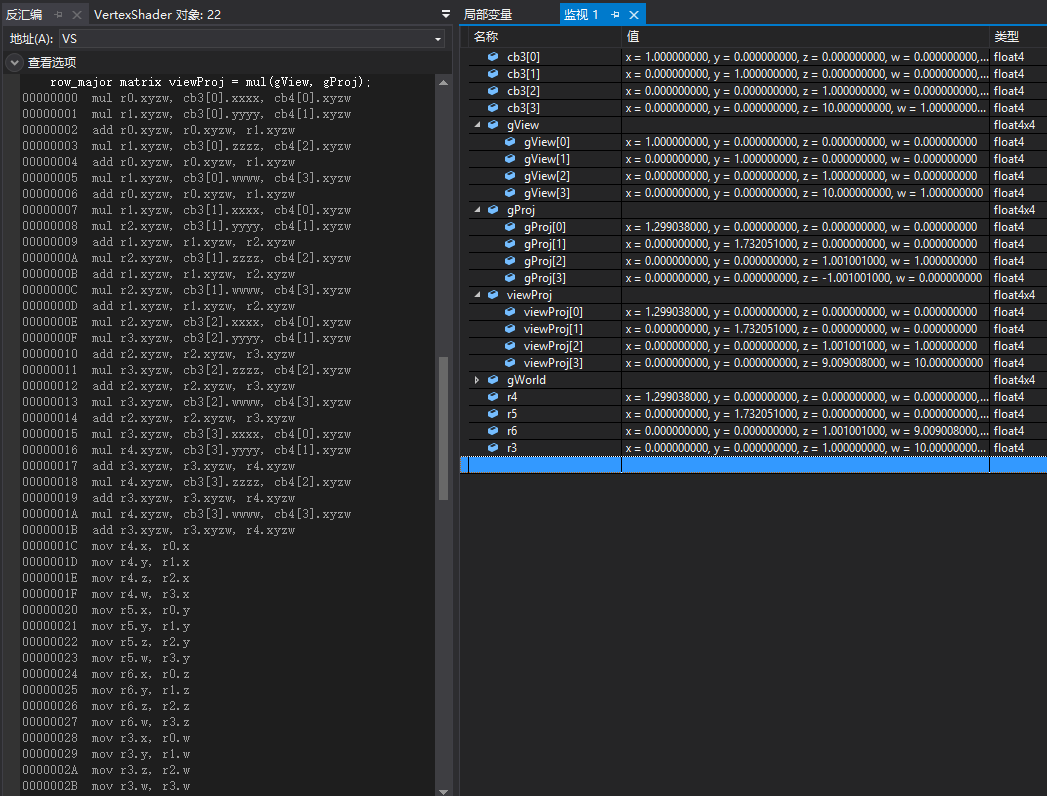
总结
综上所述,有三处地方可能会发生转置:
- C++代码端的转置
- HLSL中matrix(float4x4)是列主矩阵时会发生转置
- mul乘法内部是以列向量右乘矩阵的形式实现的,对于行向量左乘矩阵的情况会发生转置
经过组合,就一共有四种能够正常绘制的情况:
- C++代码端不进行转置,HLSL中使用
row_major matrix(行主序矩阵),mul函数让向量放在左边(行向量),这样实际运算就是(行向量 X 行主序矩阵) 。这种方法易于理解,但是这样做dp4运算取矩阵的列很不方便,在HLSL中会产生用于转置矩阵的大量指令,性能上有损失。 - C++代码端进行转置,HLSL中使用
matrix(列主序矩阵) ,mul函数让向量放在左边(行向量),这样就是(行向量 X 列主序矩阵),但C++这边需要进行一次矩阵转置,HLSL内部不产生转置 。这是官方例程所使用的方式,这样可以使得dp4运算可以直接取列主序矩阵的行,从而避免内部产生大量的转置指令。后续我会将教程的项目也使用这种方式。 - C++代码端不进行转置,HLSL中使用
matrix(列主序矩阵),mul函数让向量放在右边(列向量),实际运算是(列主序矩阵 X 列向量)。这种方法的确可行,取列矩阵的行也比较方便,效率上又和2等同,就是HLSL那边的矩阵乘法都要反过来写,然而DX本身就是崇尚行主矩阵的,把OpenGL的习惯带来这边有点。。。 - C++代码端进行转置,HLSL中使用
row_major matrix(行主序矩阵),mul函数让向量放在右边(列向量),实际运算是(行主序矩阵 X 列向量)。 就算这种方法也可以绘制出来,但还是很让人难受,比第2点还难受,我甚至不想去说它。
也就是说,以组合1为基准,任意改变其中两个状态都不会影响最终结果。
DirectX11 With Windows SDK完整目录
欢迎加入QQ群: 727623616 可以一起探讨DX11,以及有什么问题也可以在这里汇报。